菲尔兹奖得主再次突破数论难题：多少整数能写成2个有理数立方和？结论直接影响“千禧难题”之七

Pine 萧箫 发自 凹非寺

量子位 | 公众号 QbitAI

求解一共有多少整数，能被写成2个有理数（整数和分数统称）的立方和。

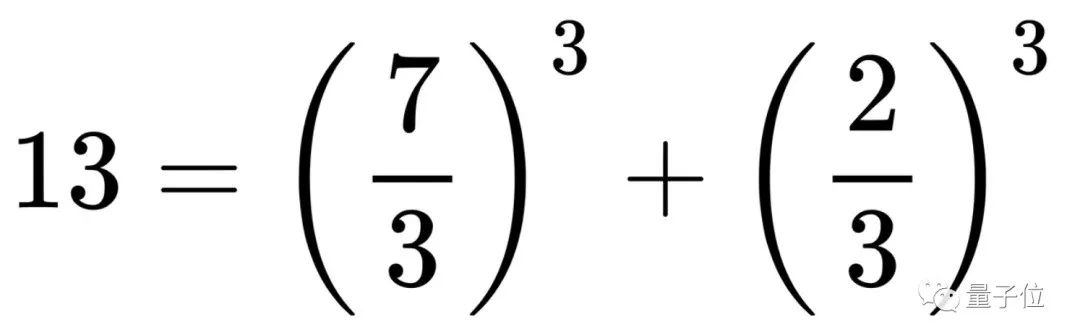
分析两个数的立方和，意味着研究的族（family，集的同义词）非常小，族越小意味着问题越难。

我只能说这个问题很难、特别难，答案几乎“遥不可及”。

所以这个数学问题究竟难在哪里，数学家们又究竟如何取得了这一突破？

选择与三次方“死磕”

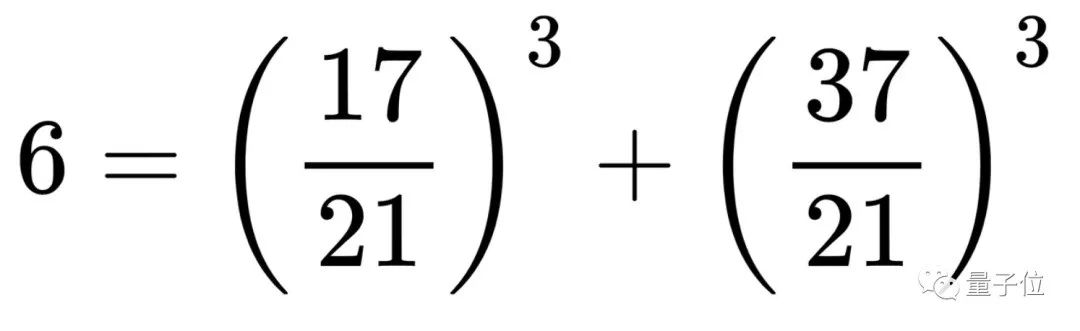
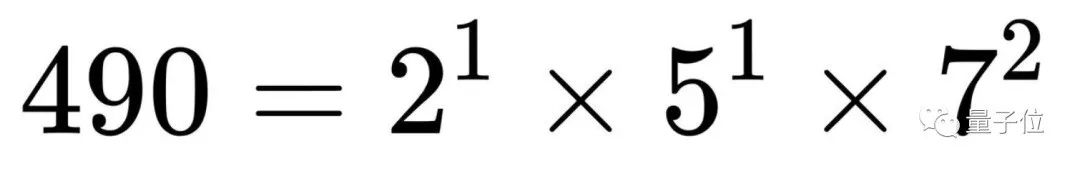
这里7除以4余3，它的指数为2，符合偶数的要求，因此整数490可以用两个有理数平方和表示：

△蓝色数字可以写成两个有理数立方之和

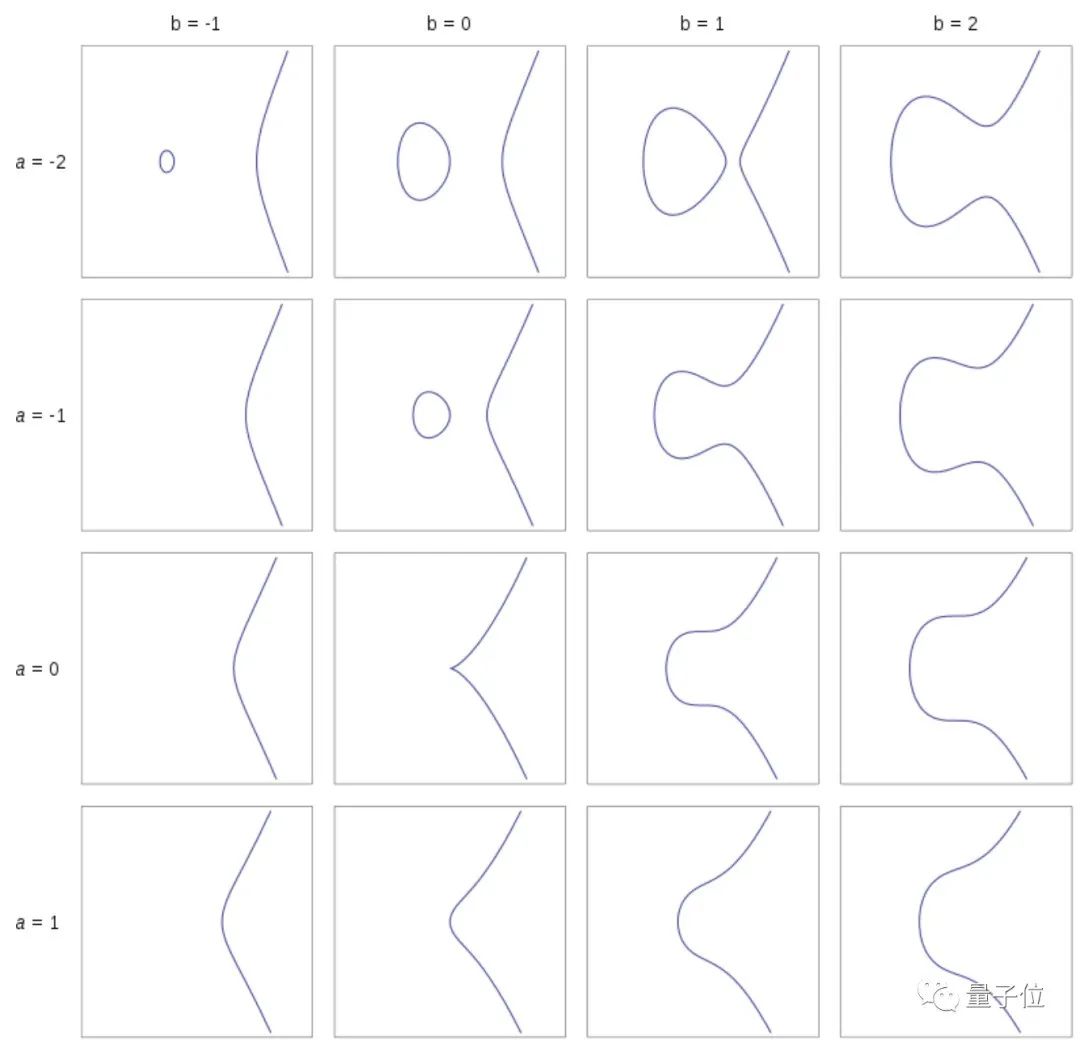
△椭圆曲线方程

椭圆曲线具有极其复杂的结构，这使它成为纯数学和应用数学等许多领域的中心，在密码学中也有很大的用处。

△椭圆曲线，图源维基百科

在1000万个数字中，约有59%是两个有理数立方的总和。