酷应用

推荐：如何比较两个或多个分布形态（附链接）

百家作者：数据分析 2022-08-18 09:56:33

作者：Matteo Courthoud 翻译：陈超校对：赵茹萱

本文约7700字，建议阅读15分钟
本文从可视化绘图视角和统计检验的方法两种角度介绍了比较两个或多个数据分布形态的方法。

从可视化到统计检验全方位分布形态比较指南：

图片来自作者

比较同一变量在不同组别之间的经验分布是数据科学当中的常见问题，尤其在因果推断中，我们经常在需要评估随机化质量时遇到上述问题。

我们想评估某一政策的效果（或者用户体验功能，广告宣传，药物，……），因果推断当中的金标准就是随机对照试验，也叫作A/B测试。在实际情况下，我们会选择一个样本进行研究，随机分为对照组和实验组，并且比较两组之间结果差异。随机化能够确保两组间唯一的差异是是否接受治疗，平均而言，以便于我们可以将结果差异归因于治疗效应。

问题是，尽管进行了随机化，两组也不会完全相同。有时，他们甚至不是“相似的”。例如，我们可能会在一组中有更多男性或年龄更大的人，等等（我们通常把这些叫做特质协变量或控制变量）。这种情况发生时，我们再也无法确定结果的差异仅仅是由治疗的效果导致，也不能将其完全归因于不平衡的协变量。因此，随机化之后非常重要的一步就是检查是否所有观测变量都是组间平衡的，是否不存在系统性差异。另外一个选择是分层抽样，额可以事先确保特定协变量是平衡的。

在本文中，我们将通过不同方式比较两组（或多组）分布并评估他们之间差异的量级和显著性水平。可视化和统计角度这两种方法通常是严谨性和直觉的权衡：从图上，我们可以迅速评估和探究差异，但是很难区分这些差异是否是系统性的还是仅仅由于噪声导致。

例子

假设我们需要将一组人随机分到处理组和对照组。我们需要让两组尽可能地相似，以便于将组间差异归因于治疗效应。我们也需要将处理组分成几个亚组来测试不同治疗的影响（例如，同一种药物的细微变化）。

对于这个例子来说，我们已经模拟了1000个被试数据集，我从src.dgp导入了数据生成过程dgp_rnd_assignment()，并从src.utils导入了一些绘图函数和库，从而观测到一系列特征。

from src.utils import *from src.dgp import dgp_rnd_assignment
df = dgp_rnd_assignment().generate_data()df.head()

数据快照，图片来自作者

我们有1000个被试的信息，从中可以观测到性别、年龄和周收入。每个被试被分配到处理组或对照组，被分到处理组的被试又被分到四种不同的治疗亚组当中去。

两组-图

让我们从最简单的情况开始：比较处理组和对照组的收入分布。首先用可视化方法来进行探究，然后再使用统计方法。可视化方法的优势在于直观，而统计方法方法的优势则在于严谨。

对大多数可视化来说，我会使用python当中的searborn库。

箱线图

第一种可视化方法是箱线图。箱线图是统计概要和数据可视化之间的很好的兑易。箱体的中心表征中位数，上下边界则表征第1和第3百分位数。须体延长到超过箱体四分位数（Q3-Q1）1.5倍的第一个数据点。落在须体之外的点则分别绘制，且通常被视作异常值。

因此，箱线图提供了统计概要（箱体和须体）以及直观的数据可视化（异常值）。

sns.boxplot(data=df, x='Group', y='Income');plt.title("Boxplot");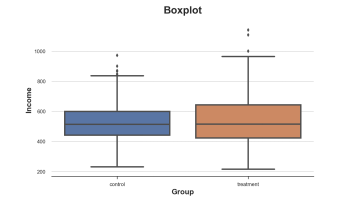

处理组合对照组的收入分布，图片来自作者

看起来处理组的收入分布更加分散：橘色箱体更大，须体覆盖范围更广。然而，箱线图的问题在于它隐藏了数据的形态，仅仅告诉我们统计概要而未向我们展示真实的数据分布情况。

直方图

直方图是展示分布最直观的方式，它将数据分成同等宽度的组，将每组观测值数量画出来。

sns.histplot(data=df, x='Income', hue='Group', bins=50);plt.title("Histogram");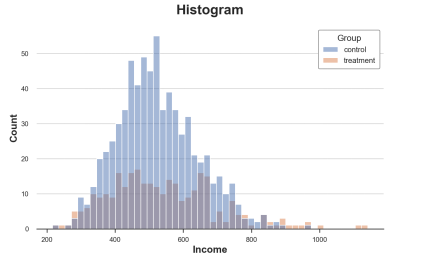

处理组和对照组的收入分布情况，图片来自作者

该图也存在很多问题：

因为两组观测值数量不同，两个直方图不具备可比性。

分组的数量是武断的。

我们可以通过stat选项来解决第一个方法，绘制density而非计数，将common_norm选项设置为False来分别对每个直方图进行归一化。

sns.histplot(data=df, x='Income', hue='Group', bins=50, stat='density', common_norm=False);plt.title("Density Histogram");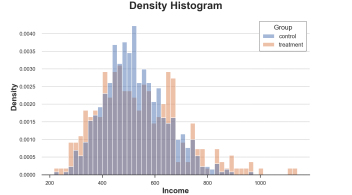

处理组和对照组的分布，图片来自作者

现在两组直方图就可比较了！

然而，一个重要的问题仍然存在：分组的大小是武断的。在极端情况下，如果我们把更少的数据捆绑在一起，最后会得到每组至多一条观测数据，如果我们把更多的数据捆绑在一起，我们最终可能会得到一个组。在两种情况下，如果我们夸大，图就会损失信息量。这就是经典的偏差-变异兑易。

核密度图

一种可能的解决方法是使用核密度函数，使用核密度估计(KDE)用连续函数近似直方图。

sns.kdeplot(x='Income', data=df, hue='Group', common_norm=False);plt.title("Kernel Density Function");

处理组和对照组收入分布，图片来自作者

从图上可以看出，似乎处理组的收入的估计核密度有“更胖的尾巴”（更高的方差），但组间均值更为相似。

核密度估计的问题自安于它是一个黑箱，可能会掩盖数据的相关特征。

累积分布图

一种更为透明的表征两个分布的方法是累积分布函数。在x轴的每个点（收入）我们绘制出数值相等或更低的数据点的百分比。累积分布函数的优势在于：

我们不需要做出任何武断的决策（例如，分组数量）
我们不需要做任何近似（例如：KDE），但是我们可以表征所有的数据点

sns.histplot(x='Income', data=df, hue='Group', bins=len(df), stat="density",element="step", fill=False, cumulative=True, common_norm=False);plt.title("Cumulative distribution function");

处理组和对照组的累积分布图，图片来自作者

我们应该如何解释这幅图？

两条线在0.5（y轴）附近交叉，意味着他们的中位数相似
在左侧橘色线在蓝色线上，而右侧则相反，意味着处理组分布的尾部更胖（极端值更多）

Q-Q图

一个相关的方法是Q-Q图，其中Q代表分位数。Q-Q图将两个分布的分位数相互绘制出来。如果分布相同，就会得到45度的直线。

Python中没有本地的Q-Q图函数，虽然statmodels包提供了一个qqplot函数，但它相当麻烦。因此，我们需要手动完成。

首先，我们需要使用percentile函数计算两组的四分位数。

income = df['Income'].valuesincome_t = df.loc[df.Group=='treatment', 'Income'].valuesincome_c = df.loc[df.Group=='control', 'Income'].valuesdf_pct = pd.DataFrame()df_pct['q_treatment'] = np.percentile(income_t, range(100))df_pct['q_control'] = np.percentile(income_c, range(100))

现在，我们可以将两个分位数分布相互对照，加上45度线，表示基准的完美拟合。

plt.figure(figsize=(8, 8))plt.scatter(x='q_control', y='q_treatment', data=df_pct, label='Actual fit');sns.lineplot(x='q_control', y='q_control', data=df_pct, color='r', label='Line of perfect fit');plt.xlabel('Quantile of income, control group')plt.ylabel('Quantile of income, treatment group')plt.legend()plt.title("QQ plot");

Q-Q 图, 图片来自作者

Q-Q图提供了与累积分布图非常相似的见解:处理组的收入有相同的中位数(在中心交叉的线)，但更宽的尾部(点在左边的线以下，右边的线以上)。

两组——检验

到目前为止，我们已经看到了可视化分布之间差异的不同方法。可视化的主要优点是直观:我们可以通过肉眼观察差异并直观地评估它们。

然而，我们可能想要更严格地评估分布之间的差异的统计意义，即回答这个问题“观察到的差异是系统的还是由于采样噪声?”

我们现在将分析不同的测试来辨别两个分布。

T检验

第一个也是最常见的检验是学生t检验。t检验通常用于比较平均值。在这种情况下，我们希望测试两组的收入分配均值是否相同。两均值比较检验的检验统计量为：

T检验统计，图片来自作者

式中为样本均值，s为样本标准差。在较温和的条件下，检验统计量是渐近分布的Student t分布。

我们使用scipy中的ttest_ind函数来执行t检验。该函数返回测试统计数据和隐含的p值。

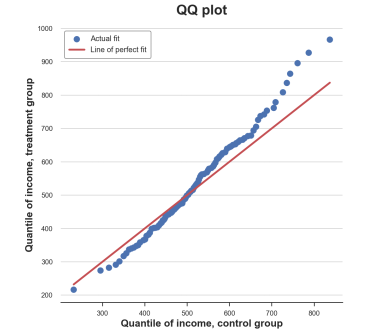
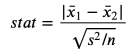
from scipy.stats import ttest_indstat, p_value = ttest_ind(income_c, income_t)print(f"t-test: statistic={stat:.4f}, p-value={p_value:.4f}")t-test: statistic=-1.5549, p-value=0.1203

检验的p值为0.12，因此我们不拒绝处理组和对照组平均值无差异的零假设。

注:t检验假设两个样本的方差相同，因此其估计是在联合样本上计算的。Welch’s t检验允许两个样本的方差不相等。

标准化均值差异（SMD）

一般来说，当我们进行随机对照试验或a /B测试时，总是对整个处理组和对照组的所有变量进行平均值差异测试是一个好做法。

然而，由于t检验统计量的分母取决于样本量，t检验因使p值难以跨研究进行比较而受到批评。事实上，我们可能在一个差异幅度很小但样本量很大的实验中获得显著的结果，而在一个差异幅度很大但样本量很小的实验中，我们可能获得不显著的结果。

已经提出的一种解决方案是标准化的均值差异(SMD)。顾名思义，这并不是一个合适的检验统计量，而只是一个标准化的差异，公式如下:

标准化均值差异，图片来自作者

通常来说，0.1以下的值可被认为是“小差异”。

最好的做法是收集处理组和对照组所有变量的平均值，以及两者之间的距离——要么t检验，要么SMD——到一个被称为平衡表的表格中。可以使用causalml库中的create_table_one函数来生成它。正如该函数的名称所暗示的那样，在执行A/B测试时，平衡表应该是您呈现的第一个表。

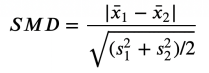
from causalml.match import create_table_onedf['treatment'] = df['Group']=='treatment'create_table_one(df, 'treatment', ['Gender', 'Age', 'Income'])

平衡表，图片来自作者

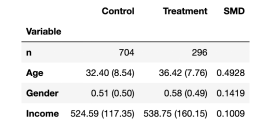
在前两列中，我们可以看到处理组和对照组不同变量的平均值，括号中是标准误差。在最后一列，SMD的值表明所有变量的标准化差异大于0.1，表明两组可能是不同的。

Mann–Whitney U 检验

另一种可选的检验是Mann–Whitney U 检验。零假设是两组有相同的粉不，而备择假设是一组的值比另一组更大（或更小）。

不同于我们之前看过的检验，Mann–Whitney U 检验不关注异常值，而把注意力放在分布的中心上。

检验流程如下。

1.将所有数据点合并排序（升序或降序）

2.计算U₁ = R₁ − n₁(n₁ + 1)/2, R₁是第一组的秩和，n₁是第一组数据的数量。

3.用相似的方法计算第二组的U₂

4.统计检验量是stat = min(U₁, U₂)

在两个分布之间没有系统秩差(即中位数相同)的零假设下，检验统计量在均值和方差已知的情况下，是渐近正态分布的。

计算R和U的直观方法是:如果第一个样品的值都大于第二个样品的值，那么R₁= n₁(n₁+ 1)/2，因此，U₁将为零(可得到的最小值)。否则，如果两个样本相似，U₁和U₂就会非常接近n₁n₂/ 2(可得到的最大值)。

我们使用来自scipy的mannwhitneyu函数执行测试。

from scipy.stats import mannwhitneyustat, p_value = mannwhitneyu(income_t, income_c)print(f" Mann–Whitney U Test: statistic={stat:.4f}, p-value={p_value:.4f}")Mann–Whitney U Test: statistic=106371.5000, p-value=0.6012

我们得到的p值为0.6，这意味着我们不拒绝零假设，即处理组和对照组的收入分配相同。

注:对于t检验，存在两样本方差不相等的Mann-Whitney U检验，即Brunner-Munzel检验。

置换检验

一种非参数选择是置换检验。其想法是，在零假设下，两种分布应该是相同的，因此混排group标签不应该显著改变任何统计量。

我们可以选择任何统计数据，并检查它在原始样本中的值与它在group标签排列中的分布如何比较。例如，让我们使用处理组和对照组之间的样本均值差异作为检验统计量。

sample_stat = np.mean(income_t) - np.mean(income_c)stats = np.zeros(1000)for k in range(1000):    labels = np.random.permutation((df['Group'] == 'treatment').values)    stats[k] = np.mean(income[labels]) - np.mean(income[labels==False])p_value = np.mean(stats > sample_stat)print(f"Permutation test: p-value={p_value:.4f}")Permutation test: p-value=0.0530

置换检验给出了0.053的p值，这意味着在5%的水平上，零假设的弱非拒绝性。

我们如何解释p值?这意味着数据中的均值差大于1-0.0560 =94.4%的排列后样本均值差。

我们可以通过绘制测试统计值与样本值之间跨排列的分布来可视化测试。

plt.hist(stats, label='Permutation Statistics', bins=30);plt.axvline(x=sample_stat, c='r', ls='--', label='Sample Statistic');plt.legend();plt.xlabel('Income difference between treatment and control group')plt.title('Permutation Test');

置换间的均值差异分布，图片来自作者

正如我们所看到的，相对于排列后的样本值，样本统计值是相当极端的，但也合理。

卡方检验

卡方检验是一个效力很强的检验，常用于检验频率差异。

卡方检验最不为人知的应用之一是检验两个分布之间的相似性。把两组观测值分组。如果这两个分布是相同的，我们将期望在每个组中有相同的观测频率。重要的是，我们需要每个组内有足够多的观测值，以保证测试的有效性。

我生成对应于对照组收入分布十分位数的组，然后计算处理组中每个组别的预期观察值频数，来确定两种分布是否相同。

# Init dataframedf_bins = pd.DataFrame()# Generate bins from control group_, bins = pd.qcut(income_c, q=10, retbins=True)df_bins['bin'] = pd.cut(income_c, bins=bins).value_counts().index# Apply bins to both groupsdf_bins['income_c_observed'] = pd.cut(income_c, bins=bins).value_counts().valuesdf_bins['income_t_observed'] = pd.cut(income_t, bins=bins).value_counts().values# Compute expected frequency in the treatment groupdf_bins['income_t_expected'] = df_bins['income_c_observed'] / np.sum(df_bins['income_c_observed']) * np.sum(df_bins['income_t_observed'])df_bins

分组和频数，图片来自作者

我们现在可以通过比较不同组别中处理组的期望值(E)和观测值(O)数来进行检验。试验统计量如下：

卡方检验统计量，图片来自作者

其中，组别由i索引，O是第i个组中观察到的数据点数量，E是第i个组中期望的数据点数量。由于我们使用对照组收入分布的十分位数来生成组别，我们预计处理组中每个组别的观察数在各个容器中是相同的。检验统计量渐近分布为卡方分布。

为了计算检验统计量和检验的p值，我们使用来自scipy的chisquare函数。

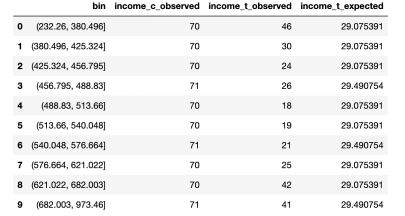
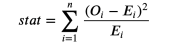
from scipy.stats import chisquarestat, p_value = chisquare(df_bins['income_t_observed'], df_bins['income_t_expected'])print(f"Chi-squared Test: statistic={stat:.4f}, p-value={p_value:.4f}")Chi-squared Test: statistic=32.1432, p-value=0.0002

与目前所有其他检验不同的是，卡方检验强烈拒绝两个分布相同的零假设。为什么?

原因在于两个分布有一个相似的中心，但尾部不同。而卡方检验检验的是整个分布的相似性，而不是像之前检验那样只在中心。

这个结果告诉我们:在从p值得出盲目结论之前，了解您实际测试的是什么是非常重要的！

Kolmogorov-Smirnov检验

Kolmogorov-Smirnov检验可能是比较分布最流行的非参数检验。Kolmogorov-Smirnov检验的思想是比较两组的累积分布。特别是，Kolmogorov-Smirnov检验统计量是两个累积分布之间的最大绝对差值。

Kolmogorov-Smirnov检验统计量,图片来自作者

其中F₁和F₂为两个累积分布函数，x为基础变量的值。Kolmogorov- smirnov检验统计量的渐近分布是Kolmogorov分布。

为了更好地理解检验，让我们画出累积分布函数和检验统计量。首先，我们计算累积分布函数。

df_ks = pd.DataFrame()df_ks['Income'] = np.sort(df['Income'].unique())df_ks['F_control'] = df_ks['Income'].apply(lambda x: np.mean(income_c<=x))df_ks['F_treatment'] = df_ks['Income'].apply(lambda x: np.mean(income_t<=x))df_ks.head()

累计分布数据集快照，图片来自作者

我们现在需要找到累积分布函之间的绝对距离最大的点。

k = np.argmax( np.abs(df_ks['F_control'] - df_ks['F_treatment']))ks_stat = np.abs(df_ks['F_treatment'][k] - df_ks['F_control'][k])

我们可以通过绘制两个累积分布函数和测试统计量的值来可视化测试统计量的值。

y = (df_ks['F_treatment'][k] + df_ks['F_control'][k])/2plt.plot('Income', 'F_control', data=df_ks, label='Control')plt.plot('Income', 'F_treatment', data=df_ks, label='Treatment')plt.errorbar(x=df_ks['Income'][k], y=y, yerr=ks_stat/2, color='k',capsize=5, mew=3, label=f"Test statistic: {ks_stat:.4f}")plt.legend(loc='center right');plt.title("Kolmogorov-Smirnov Test");

Kolmogorov-Smirnov检验统计量,图片来自作者

从图中，我们可以看到检验统计量的值对应于收入~650处两个累积分布之间的距离。就收入价值而言，两组之间的不平衡是最大的。

现在我们可以使用来自scipy的kstest函数执行实际的测试。

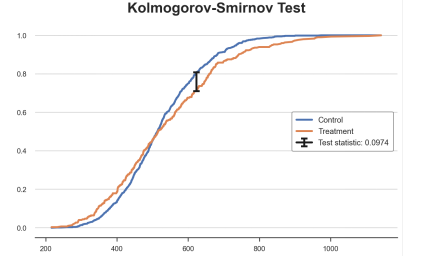
from scipy.stats import ksteststat, p_value = kstest(income_t, income_c)print(f" Kolmogorov-Smirnov Test: statistic={stat:.4f}, p-value={p_value:.4f}")Kolmogorov-Smirnov Test: statistic=0.0974, p-value=0.0355

p值低于5%:我们以95%的置信度拒绝两个分布相同的零假设。

注1:KS检验过于保守，很少拒绝零假设。Lilliefors检验使用测试统计量的不同分布(Lilliefors分布)校正了这一偏差。

注2:KS测试使用的信息很少，因为它只比较在一点上的两个累积分布:最大距离的一个。Anderson-Darling检验和Cramér-von Mises检验通过积分来比较整个域上的两个分布(两者之间的差异在于平方距离的加权)。

多组-图

到目前为止，我们只考虑了两组的情况:处理组和对照组。但如果我们有多个组呢?我们看到的一些方法可以很好地扩展，而另一些则不行。

作为一个可行的例子，我们现在要检查不同处理组的收入分布是否相同。

箱线图

当我们有许多个位数的组时，箱线图可以很好地缩放，因为我们可以把不同的盒子并排放在一起。

sns.boxplot(x='Arm', y='Income', data=df.sort_values('Arm'));plt.title("Boxplot, multiple groups");

不同处理亚组收入分布，图片来自作者

从图中可以看出，不同组别的收入分布是不同的，编号越高的组别平均收入越高。

小提琴图

结合了汇总统计和核密度估计的箱线图的一个很好的扩展是小提琴图。小提琴图显示了沿y轴的独立密度，所以他们不会重叠。默认情况下，它还在内部添加一个微型箱线图。

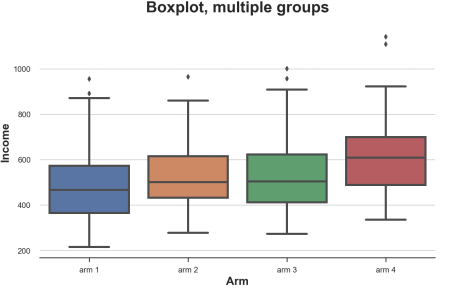
sns.violinplot(x='Arm', y='Income', data=df.sort_values('Arm'));plt.title("Violin Plot, multiple groups");

不同处理亚组收入分布，图片来自作者

相较于箱线图，小提琴图能表明不同处理组的收入不同。

脊线图

最后，脊线图沿x轴绘制多个核密度分布，比小提琴图更直观，但部分重叠。不幸的是，在matplotlib和seaborn中都没有默认的脊线图。我们需要从joypy导入它。

from joypy import joyplotjoyplot(df, by='Arm', column='Income', colormap=sns.color_palette("crest", as_cmap=True));plt.xlabel('Income');plt.title("Ridgeline Plot, multiple groups");

不同处理亚组收入分布，图片来自作者

同样，脊线图表明，编号越高的治疗组收入越高。从这个图中，也更容易理解分布的不同形状。

多组-检验

最后，让我们考虑假设检验来比较多个组。为了简单起见，我们将集中讨论最常用的一个:F检验。

F-检验

对于多个组，最常用的测试是f测试。f检验比较一个变量在不同组之间的方差。这种分析也被称为方差分析，或ANOVA。

在实际应用中，F检验统计量由

F检验统计量，图片来自作者

其中G为组数，N为观察次数，为总体均值，g为g组内均值。在组独立性零假设下，f统计量为F分布。

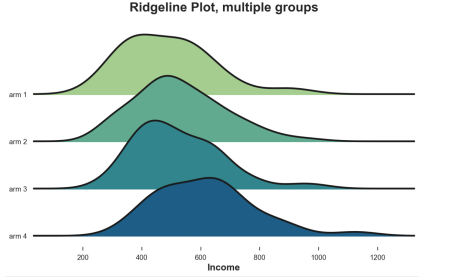
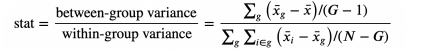
from scipy.stats import f_onewayincome_groups = [df.loc[df['Arm']==arm, 'Income'].values for arm in df['Arm'].dropna().unique()]stat, p_value = f_oneway(*income_groups)print(f"F Test: statistic={stat:.4f}, p-value={p_value:.4f}")F Test: statistic=9.0911, p-value=0.0000

检验p值基本为零，这意味着强烈拒绝零假设，即各治疗组之间的收入分配没有差异。

结论

在这篇文章中，我们已经看到了大量不同的方法来比较两个或多个分布，无论是视觉上的还是统计上的。这是许多应用的主要关注点，在因果推断中尤其如此，我们使用随机化方法使处理组和对照组尽可能具有可比性。

我们还看到不同的方法可能更适合不同的情况。可视化方法有助于建立直觉，但统计方法对于决策至关重要，因为我们需要能够评估差异的量级和统计意义。

参考文献

[1] Student, The Probable Error of a Mean (1908), Biometrika.

[2] F. Wilcoxon, Individual Comparisons by Ranking Methods (1945), Biometrics Bulletin.

[3] B. L. Welch, The generalization of “Student’s” problem when several different population variances are involved (1947), Biometrika.

[4] H. B. Mann, D. R. Whitney, On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other (1947), The Annals of Mathematical Statistics.

[5] E. Brunner, U. Munzen, The Nonparametric Behrens-Fisher Problem: Asymptotic Theory and a Small-Sample Approximation (2000), Biometrical Journal.

[6] A. N. Kolmogorov, Sulla determinazione empirica di una legge di distribuzione (1933), Giorn. Ist. Ital. Attuar..

[7] H. Cramér, On the composition of elementary errors (1928), Scandinavian Actuarial Journal.

[8] R. von Mises, Wahrscheinlichkeit statistik und wahrheit (1936), Bulletin of the American Mathematical Society.

[9] T. W. Anderson, D. A. Darling, Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes (1953), The Annals of Mathematical Statistics.

相关文章

再见散点图,欢迎统计分组（binned）散点图

（https://towardsdatascience.com/controls-b63dc69e3d8c）

代码

您可以点击下方网址查看原始 Jupyter Notebook:

https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/distr.ipynb

原文标题：

How to Compare Two or More Distributions

原文链接：

https://towardsdatascience.com/how-to-compare-two-or-more-distributions-9b06ee4d30bf

译者简介：陈超，北京大学应用心理硕士在读。本科曾混迹于计算机专业，后又在心理学的道路上不懈求索。越来越发现数据分析和编程已然成为了两门必修的生存技能，因此在日常生活中尽一切努力更好地去接触和了解相关知识，但前路漫漫，我仍在路上。

END