为什么要做特征的归一化/标准化?
本文约4300字,建议阅读8分钟 本文探索对于feature scaling中最常使用的Standardization。
写在前面
Feature scaling,常见的提法有“特征归一化”、“标准化”,是数据预处理中的重要技术,有时甚至决定了算法能不能work以及work得好不好。谈到feature scaling的必要性,最常用的2个例子可能是:
特征间的单位(尺度)可能不同,比如身高和体重,比如摄氏度和华氏度,比如房屋面积和房间数,一个特征的变化范围可能是[1000, 10000],另一个特征的变化范围可能是[?0.1,0.2],在进行距离有关的计算时,单位的不同会导致计算结果的不同,尺度大的特征会起决定性作用,而尺度小的特征其作用可能会被忽略,为了消除特征间单位和尺度差异的影响,以对每维特征同等看待,需要对特征进行归一化。 原始特征下,因尺度差异,其损失函数的等高线图可能是椭圆形,梯度方向垂直于等高线,下降会走zigzag路线,而不是指向local minimum。通过对特征进行zero-mean and unit-variance变换后,其损失函数的等高线图更接近圆形,梯度下降的方向震荡更小,收敛更快,如下图所示,图片来自Andrew Ng。

Feature Scaling from Andrew Ng
常用的feature scaling方法都有哪些? 什么情况下该使用什么feature scaling方法?有没有一些指导思想? 所有的机器学习算法都需要feature scaling吗?有没有例外? 损失函数的等高线图都是椭圆或同心圆吗?能用椭圆和圆来简单解释feature scaling的作用吗? 如果损失函数的等高线图很复杂,feature scaling还有其他直观解释吗?
常用feature scaling方法

feature matrix
Rescaling (min-max normalization、range scaling):

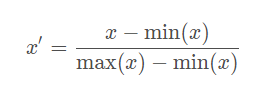
Mean normalization:

Standardization (Z-score Normalization):

Scaling to unit length:
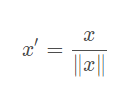
计算方式上对比分析
减一个统计量可以看成选哪个值作为原点,是最小值还是均值,并将整个数据集平移到这个新的原点位置。如果特征间偏置不同对后续过程有负面影响,则该操作是有益的,可以看成是某种偏置无关操作;如果原始特征值有特殊意义,比如稀疏性,该操作可能会破坏其稀疏性。 除以一个统计量可以看成在坐标轴方向上对特征进行缩放,用于降低特征尺度的影响,可以看成是某种尺度无关操作。缩放可以使用最大值最小值间的跨度,也可以使用标准差(到中心点的平均距离),前者对outliers敏感,outliers对后者影响与outliers数量和数据集大小有关,outliers越少数据集越大影响越小。 除以长度相当于把长度归一化,把所有样本映射到单位球上,可以看成是某种长度无关操作,比如,词频特征要移除文章长度的影响,图像处理中某些特征要移除光照强度的影响,以及方便计算余弦距离或内积相似度等。
 Standardization
Standardization


feature scaling 需要还是不需要
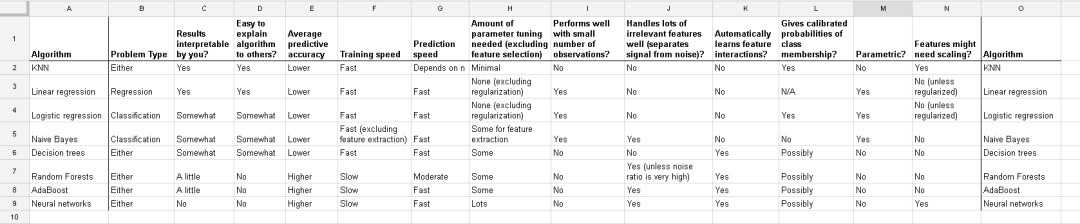
Comparing supervised learning algorithms
什么时候需要feature scaling?
涉及或隐含距离计算的算法,比如K-means、KNN、PCA、SVM等,一般需要feature scaling,因为:
损失函数中含有正则项时,一般需要feature scaling:对于线性模型y=wx+b而言,x的任何线性变换(平移、放缩),都可以被w和b“吸收”掉,理论上,不会影响模型的拟合能力。但是,如果损失函数中含有正则项,如λ∣∣w∣∣^2,λ为超参数,其对w的每一个参数施加同样的惩罚,但对于某一维特征xi而言,其scale越大,系数wi越小,其在正则项中的比重就会变小,相当于对wi惩罚变小,即损失函数会相对忽视那些scale增大的特征,这并不合理,所以需要feature scaling,使损失函数平等看待每一维特征。 梯度下降算法,需要feature scaling。梯度下降的参数更新公式如下,

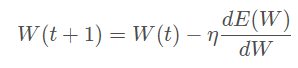

Gradient descent for different learning rates
zero center与参数初始化相配合,缩短初始参数位置与local minimum间的距离,加快收敛。模型的最终参数是未知的,所以一般随机初始化,比如从0均值的均匀分布或高斯分布中采样得到,对线性模型而言,其分界面初始位置大致在原点附近,bias经常初始化为0,则分界面直接通过原点。同时,为了收敛,学习率不会很大。而每个数据集的特征分布是不一样的,如果其分布集中且距离原点较远,比如位于第一象限遥远的右上角,分界面可能需要花费很多步骤才能“爬到”数据集所在的位置。所以,无论什么数据集,先平移到原点,再配合参数初始化,可以保证分界面一定会穿过数据集。此外,outliers常分布在数据集的外围,与分界面从外部向内挪动相比,从中心区域开始挪动可能受outliers的影响更小。 对于采用均方误差损失LMS的线性模型,损失函数恰为二阶,如下图所示 另有从Hessian矩阵特征值以及condition number角度的理解,详见Lecun paper-Efficient BackProp中的Convergence of Gradient Descent一节,有清晰的数学描述,同时还介绍了白化的作用——解除特征间的线性相关性,使每个维度上的梯度下降可独立看待。 文章开篇的椭圆形和圆形等高线图,仅在采用均方误差的线性模型上适用,其他损失函数或更复杂的模型,如深度神经网络,损失函数的error surface可能很复杂,并不能简单地用椭圆和圆来刻画,所以用它来解释feature scaling对所有损失函数的梯度下降的作用,似乎过于简化,见Hinton vedio-3.2 The error surface for a linear neuron。 对于损失函数不是均方误差的情况,只要权重w与输入特征x间是相乘关系,损失函数对w的偏导必然含有因子x,w的梯度下降速度就会受到特征x尺度的影响。理论上为每个参数都设置上自适应的学习率,可以吸收掉x尺度的影响,但在实践中出于计算量的考虑,往往还是所有参数共用一个学习率,此时x尺度不同可能会导致不同方向上的下降速度悬殊较大,学习率不容易选择,下降过程也可能不稳定,通过scaling可对不同方向上的下降速度有所控制,使下降过程相对更稳定。 对于传统的神经网络,对输入做feature scaling也很重要,因为采用sigmoid等有饱和区的激活函数,如果输入分布范围很广,参数初始化时没有适配好,很容易直接陷入饱和区,导致梯度消失,所以,需要对输入做Standardization或映射到[0,1]、[?1,1],配合精心设计的参数初始化方法,对值域进行控制。但自从有了Batch Normalization,每次线性变换改变特征分布后,都会重新进行Normalization,似乎可以不太需要对网络的输入进行feature scaling了?但习惯上还是会做feature scaling。
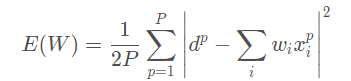
什么时候不需要Feature Scaling?
小结
END
版权声明:本号内容部分来自互联网,转载请注明原文链接和作者,如有侵权或出处有误请和我们联系。
合作请加QQ:365242293??
数据分析(ID?:?ecshujufenxi?)互联网科技与数据圈自己的微信,也是WeMedia自媒体联盟成员之一,WeMedia联盟覆盖5000万人群。

关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/
 关注网络尖刀微信公众号
关注网络尖刀微信公众号随时掌握互联网精彩
赞助链接
排名
热点
搜索指数
- 1 中央经济工作会议在北京举行 7904216
- 2 紧急提醒:请在日中国公民进行登记 7808031
- 3 中央定调明年继续“国补” 7711798
- 4 “九天”无人机成功首飞 7619127
- 5 断崖式降温!今冬最强寒潮来了 7521995
- 6 中央经济工作会议释信号:3件事不做 7424553
- 7 4人喝近120瓶啤酒惊呆老板 7331256
- 8 一粒米盖住6个字 药品说明书该改了 7238915
- 9 人民空军中日双语发文:大惊小怪 7141366
- 10 寒潮来袭 “速冻”模式如何应对 7048706



![宁宁子同学 黑长直还是双马尾呢? [抱一抱]](https://imgs.knowsafe.com:8087/img/aideep/2023/9/24/4747a5cd43d33b67a1a9eb30ccba8f94.jpg?w=250)



 数据分析
数据分析







