酷应用

推荐：115个A/B测试的分析结果︰平均提升为4%，大部分缺乏统计检定力

百家作者：数据分析 2021-10-11 23:15:16

作者 : Georgi Georgiev 翻译：Gabriel Ng 校对：张玲


本文约6400字，建议阅读10分钟
本文讨论初始数据必要的修剪，然后分享元分析的详细结果，最后作出一个简短的总结。

从115个公开的A/B测试中你能够得到什么信息？通常情况下并不会太多，原因在于大部分情况下，你只能看到有关被测对象的基本数据和A/B测试结果。另一方面，置信区间、p值以及其他针对不确定性的度量则往往被遗忘，而即使有，它们的计算也不尽人意，又或者背后的统计过程没有分享出来，使得它们实际上难以使用。一个数据来源︰GoodUI.org有稍微好一点的方法，在他们网站上发布的每一个测试都附上了基本的统计信息︰用户数量、每个测试变量的转换以及被试对象是什么。

笔者决定收集这些数据，并对这115个测试（在下文展示）进行统计上的元分析。除了对A/B测试或转换率优化活动的样本的平均结果作出总结以外，这样做更多的是为了在设计和分析A/B测试时，能作为一个更好的统计习惯的指引。

一个主要发现是相对于预期的结果和成本经济逻辑，大约70%的测试有着低下的检定力，暗示着有自选停止的问题。经过数据修剪和统计上的调整后，余下的85个测试显示出4%以下的平均值和中位数相对提升，当中统计显著的平均值为6.78%，中位数为5.96%。

因为GoodUI这个样本并不能代表所有完成的A/B测试，所以对于整个A/B测试流程的任何形式的一般化都应该谨慎处理。

笔者首先会讨论初始数据必要的修剪，然后分享元分析的详细结果，最后作出一个简短的总结。

统计意义上的重新计算和数据修剪

GoodUI上的数据有对统计显著度的计算和置信区间，同时也有结果的自评︰"不显著"、"有可能"、"显著"、"强"，两个方向都有。数据也包含了所观察到的百分比改变。因为有报告的样本大小，也能对检定力作出计算。

以百分比变化形式展示，整个数据集的观察效应估计分布如下︰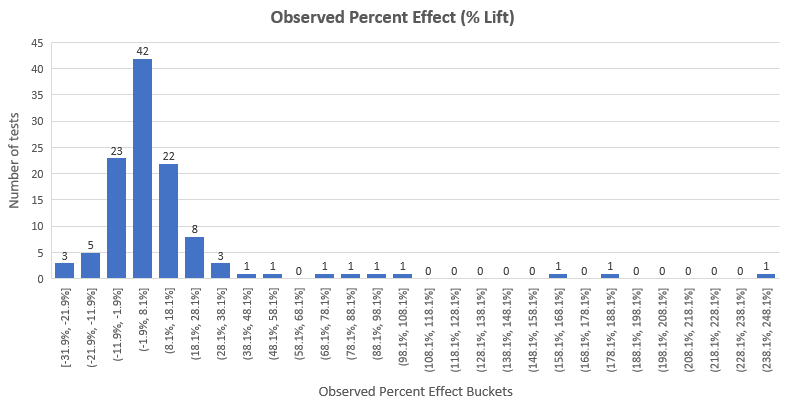

我们可以看到，结果几乎服从正态分布，效应提升的平均值在12.33%，除了右边有重尾分布。这个问题我们在下面的文章会展开讨论。效应提升的中位数是4.89%，代表着在50%的测试中观测到的效应提升小于4.89%，而真实的效应提升可能更小。注意这里也包含了那些没有通过95%显著性检验的测试的观察效应提升。

统计显著度和置信区间的重新计算

很不幸的是，在人工提取每个测试的用户数目和转换后，笔者需要优先重新计算统计显著度(p值)和置信区间的上下限，原因是网站上的统计信息有两个问题︰

1. 显著度和置信区间的计算都是以双边对立假设，而非单边对立假设作为基本，而在进行方向性的推断时，显然单边对立假设更合理。

2. p值(统计显著度)和置信区间是为了计算绝对差异，但推断目标却是百分比改变（百分比提升）。因此，笔者用了恰当的p值和置信区间来表示百分比提升。

第一个重新计算有着较预期少的不确定性，而第二个重新计算则有着较预期高的不确定性。整体上，相较原来的显著性水平和置信区间，重新计算使得不确定性减少，原因在于单边对立假设的修正抹除了百分比提升的改正。

我们可以看到，115个测试中有18个测试结果重新评级︰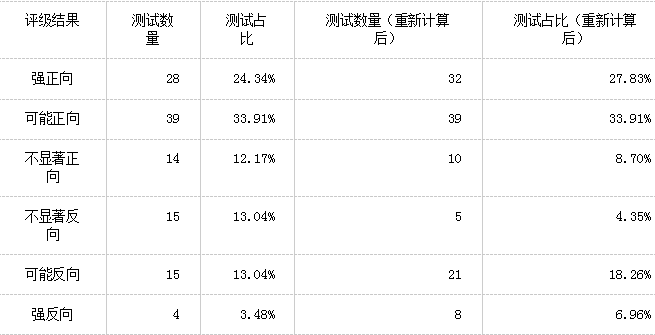

根据GoodUI的定义，有︰

p值小于等于0.03为强结果，p值小于等于0.25为可能结果，p值大于0.25为不显著结果。每一个评级结果都是连续的（例如若果p值为0.01，则测试的评级不能同时为强和可能）。GoodUI也定义了每个评级所需要的样本大小，但这是不合理的，因为p值的恰当计算包括了样本大小的调整，这比GoodUI粗略的做法来得好。

按照更为经典的p值阈值︰0.05（95%置信度），我们获得了45个统计上显著的成功结果和12个统计上显著的失败结果（分别为整体测试的39.13%和10.43%），余下的58个测试（50.44%）则有着不显著的结果。恰当p值的分布如下︰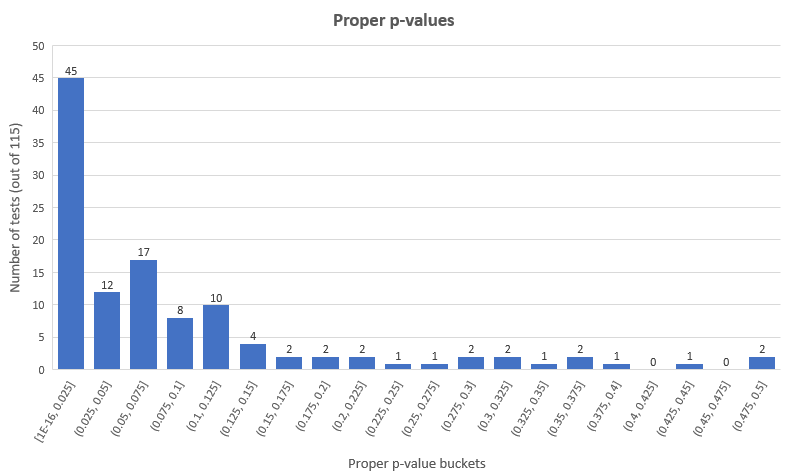

这是p值在0.05以下的测试的观测效应，恰当计算后，提升效应百分比的单尾p值如下：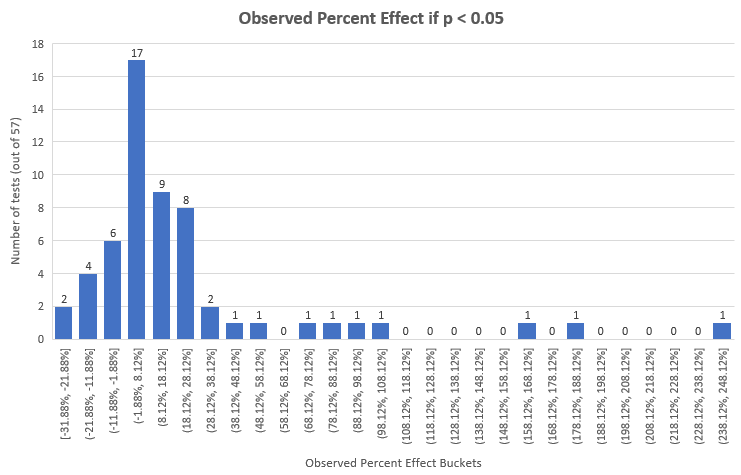

当然，比起整体，这些测试有着较高的平均值和中位数︰22.94%和7.91%，但它们只占115个中的57个。

不平衡测试的移除

115个的测试中的3个（#55，#72，#90）在对照组和实验组的用户数目上有着显著的不平衡。在第一个情景中，相较于对照组（样本大小为每组200,000+），实验组有着16%更多的用户数，而在其后的两个情景中，分别为9%和13%更少的用户数（样本大小为20,000+和10,000+）。我们可以猜测以下原因︰不恰当的随机化、技术问题引致一部分用户没有体验整体实验、采用了如多臂老虎机或在测试期间重新平衡臂的类似方法等等。

唯一合理的解释是随机化过程中，实验组和对照组流量分配不均，数量如此之多，以至于笔者怀疑就是这么回事。

如果原因是以上任何一种不合理的解释，那么很明显地任何以这一数据为基本的统计分析都会是带有偏差的。由于出现了妥协性随机化，并且笔者高度怀疑有意的不均等分布，笔者决定在最后的分析中移除以上3个测试。

明显妥协性测试的移除

在对A/B测试进行统计设计和分析时，一个常见的问题是在没有任何统计上的调整下，多次地重复窥探数据，以获得所需要和希望的数据。这种方法一般被称为︰”显著度等待”。

只需几次观察就能大大地提高显著(名义上的)结果的似然性好几倍，即使真实的观察可能性非常低。举个例子，一个有着实际上0.08p值的测试，在经过5次窥探后，就可以得到一个名义上的0.025 p值，这里实际上的p值大大偏离了0.05阈值，且是名义上的p值的3.2倍。现在我们有多种方法去观察收集数据，而其中一种是”敏捷A/B测试方法”。

发现妥协性测试的一种方法是寻找检定力低得不切实际的测试。我们可以通过询问自己以下问题来达到这一效果︰如果我正在设计测试时，考虑到干预的规模、 X%真实提升的预期效益、固定成本、可变成本等等，我会对什么样的功效水平感到满意（在文章Risk vs. Reward in A/B Tests: A/B testing as Risk Management一文中有详细介绍怎样选择合适的样本大小检定力和显著性水平）。

举例说，没有人会在变量只有轻微改变（例如按钮的内容文字）的情况下，去设计一个有着90%检定力，去侦测20%相对变化的测试。在这种情况下，去预期干预有着巨大程度的结果是不现实的，也会因为测试的检定力低下而白白浪费测试资源。所以当人们在决定合理样本大小和最小可检测效应时，一个应该自问的问题是︰怎么样的结果是令我们鼓舞的？是1%，2%，5%，还是20%？问题的答案因测试而异，但在A/B测试中很少会高于10%。

因为上述原因，合理的设计者不会在大于40%的最小可检测效应（Minimum detectable effect, MDE）情况下，设计有着90%检定力的A/B测试，原因是这会使得侦测任何低于MDE的真实效应的机会变得非常低。这一点从熟悉的”效应大小/检定力函数”的图像中就能看到。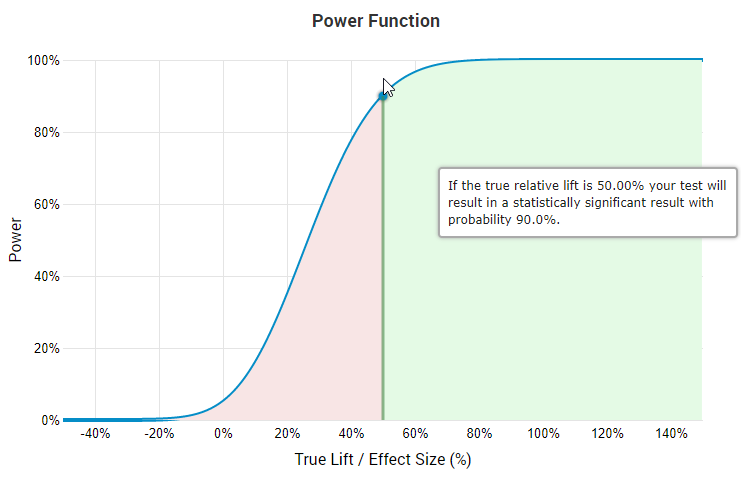

如果真实相对提升为50%，那么根据图像，测试会有90%的机会有着显著结果。

上图来源是A/B测试统计计算器，在图中能看到如果要以90%检定力去侦测50%的真实提升，那么只有45.7%的可能性侦测到25%的真实提升，且对于越小的真实效应，其可能性也越小。笔者并不对在这些水平下仍经济上合理的测试感兴趣。而且对于大部分测试，即使是在数据修剪前效应大小的中位数也有着4%-5%。这进一步说明在显著高的水平下设计有着最小可检测效应的测试是不合理的。

所以如果我们希望在115个测试中侦测出妥协性测试，在90%检定力下，观测测试效应大小的分布是一个值得的举动。下图是实际结果（平均最小可检测提升是27.8%，中位数是20.84%）︰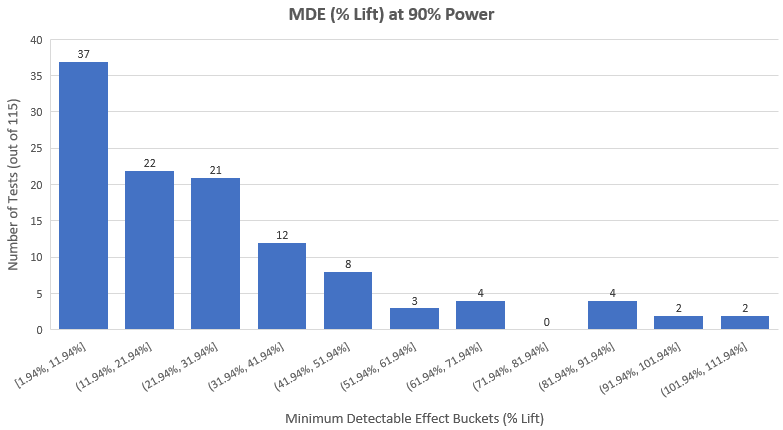

第一眼就明显的情况是︰

1. 有一大堆测试，它们的设计者认为测试有天文级别的改善效果。

2. 有一大堆测试，只有在天文级别高的结果下才经济合算。

3. 有一大堆人在没有固定样本大小的前提下进行测试，而且常常窥探数据，最后若无其事地分析结果。

笔者认为情况3最有机会代表大部分的测试。即使没有像情况3那样做，他们也是用了某种恰当的相继性分析。正确的测试是这样的︰p值的计算吻合固定样本大小测试的计算结果，而且它们只有在固定样本大小的测试下才变得合理。

通过对每一个测试的干预进行人工检视，结合笔者对于在这些干预中的合理效应大小的知识，以及A/B测试的经济效益。笔者得出了自己（某程度上的主观）的评估结果，在115个测试中的80个（69.57%）是低检定力的，从而笔者怀疑当中有不同程度的自选停止。这里，笔者必须指出其假设已经是相当宽松的。

虽然如此，笔者仍无意为了阐释评估结果中的主观部分，而单单对30个测试作出分析，故笔者决定只移除最为明显的出错例子︰在90%检定力和0.05（95%信赖度）显著水平的情况下，有着最小可检测提升为大于等于40%的测试。注意，笔者在检定力的计算中已是十分宽松，因为在GoodUI的分类中，p值的阈值为0.03，而不是0.05。

数据修剪的结果是，有25个测试被移除，因未解释的自选停止（数据窥探）下而出现了明显的妥协行为。因为没有关于窥探次数和时间的信息，我们没有办法去对p值和信赖区间作出调整以抵偿数据的窥探。被移除的总测试数变成28（当中3个是因为不平衡的样本大小），可供分析的测试有87个。

从A/B测试的角度分析多元测试

笔者遇到的另一个问题是如何把多元测试（一个对照对比多个变量）表达成两个分别的A/B测试。笔者认为这是可能的，因为两者的对照完全一致，且多元测试和两个连续的测试有着相同的样本大小和转换率。有一篇博客文章完整描述了其中一个测试的整个实验，结果表明，不单单是一个多元测试，还有未被提及的其他变量。因为在多元测试中，为了反映对照是和多个变量进行测试，我们需要调整p值和置信区间。这里便出现了问题，因为我们不能简单地进行成对的t检定或z检定，就像GoodUI中对一个个变量和对照进行p值计算。

p值和信赖区间的有效性所导致的后果和无从发现的数据窥探的后果相似︰相较报告中名义上的可能性，实际观察结果的可能性会更高。由于笔者并不知道在每一个A/B测试中有多少个变量，所以不能够对结果和最小可检测效应的计算进行Dunnett修正。笔者知道其中两个测试（#16和#17）的变量数目和它们的效应大小大于40%，暗示着它们有未解释的自选停止情况，故笔者决定把这两个测试移除。

笔者决定保留余下的测试，因为它们大部分在有着1至2个额外变量的假设下，仍然适当地保持了检定力。

A/B测试的元分析结果

115个测试的元分析结果明显有一部分测试（80=69.57%）欠缺统计检定力，有着或多或少严重的方法论问题。其中，有27个测试因明显妥协性测试而被移除。3个测试有着对照组和实验组在人流分配上的显著不平衡，故为了避免使用因技术上的可能问题而导致的偏差数据，这3个测试也被移除。16个测试是8个多元测试分拆的结果，即使如此，我们仍决定有能力能合理地评估它们的误差控制，它们当中的2个被移除，余下的则继续用作分析（有争议的决定）。

在移除3个不平衡随机化的测试和27个因缺乏固定样本大小和无从发现的数据窥探，导致统计上明显妥协的测试后，能进入元分析的测试有85个。（初始有115个）。

85个测试的平均百分比提升是3.77%，而中位数提升是3.92%，其分布如下︰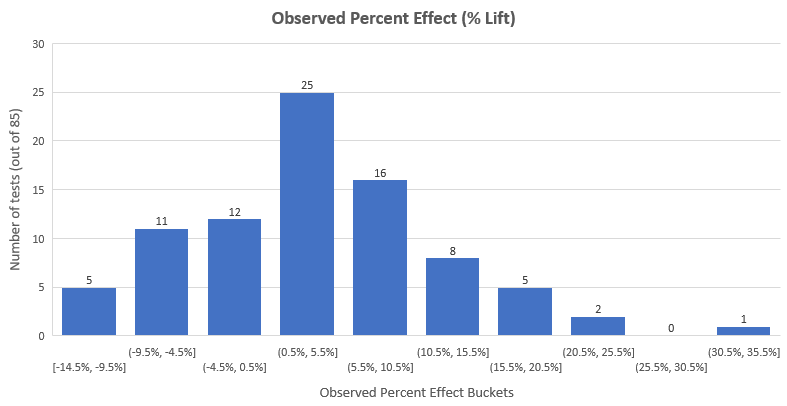

上面的分布与有着平均值3.77%的正态分布十分相似，大部分的效应（58%）在-3%和+10%之间。可以看到，在数据修剪后大部分的极端高的结果都被移除，在最初的数据集中有8个效应大于35%。这是因为在极端早的结果中，测试往往是在数据窥探、极端大的提升下就被早早停止。自然而然，这些结果也有着极端的不确定性。

大部分效应在10%提升以下的这一事实进一步支持大部分测试的检定力低下的论点，因为在115个测试中只有24个测试在90%检定力和95%显著度下，有着小于10%的最小可检定效应。

统计上显著（p<0.05）的测试的观察效应大小为︰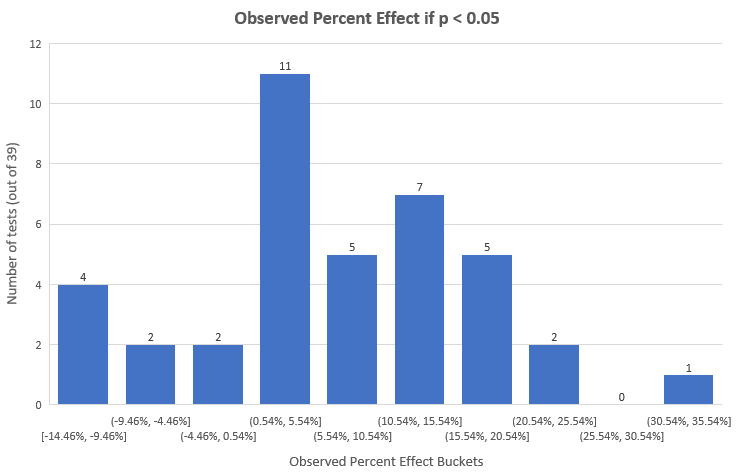

大部分测试的结果都落在0.54%-5.54%这一区间，而主体结果则在0.54%和20.54%之间。对于统计上显著的测试，它们的观察效应大小的算术平均值为6.78%的提升，当中50%的测试结果少于5.96%，而这些来自统计上显著的结果的效应大小自然地相较整体来得大。

85个测试的p值分布如下︰

可以看到在85个测试中，只有39个（45.88%）有统计上显著的结果，当中8个是负值结果，大部分测试（20个）的p值落在0.05-0.1的范围。

当有这么一大部分的测试没有达到常用的显著度阈值时，不禁令人怀疑当中出现了什么问题。直接把它们视作无价值的测试而丢弃显然不是个好做法。一般来说，我们会通过观察检定力和最小可检测效应进行分析，以下是85个测试的最小可检测效应的分布︰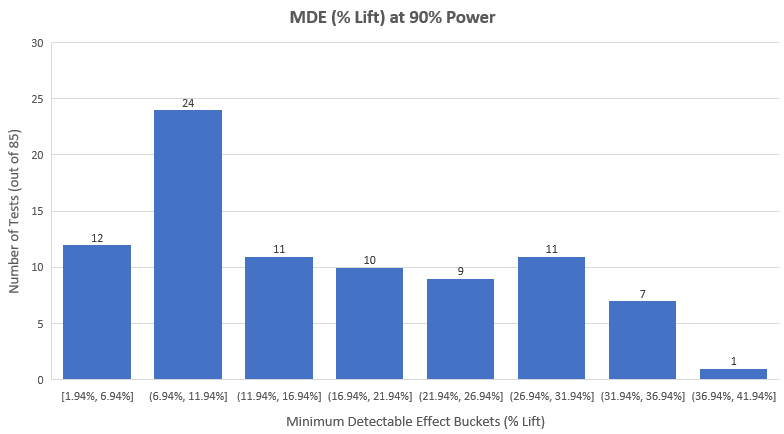

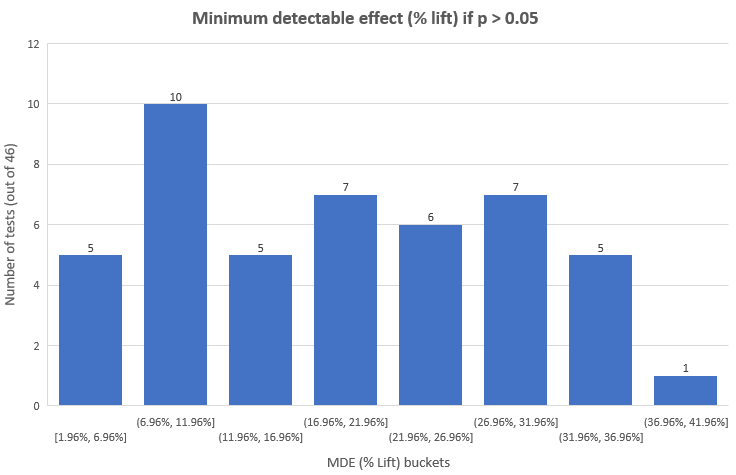
然后是在0.05阈值下不显著的测试的分布︰

我们可以看到只有46个不显著测试中的15个（32.6%）有着低于12%的最小可检测效应。对于这些测试我们可以把有着90%可能性的12%或更大的效应大小排除掉。但对于余下的25个测试，因为它们的最小可检测效应非常大，以至于对它们的排除并不会带来新的情报︰这些测试的干预程度使得如此大的效应变得几近不可能出现。

另一个更加直觉地评估没有被排除的效应大小（被置信区间覆盖的效应大小）的方法是观察置信区间︰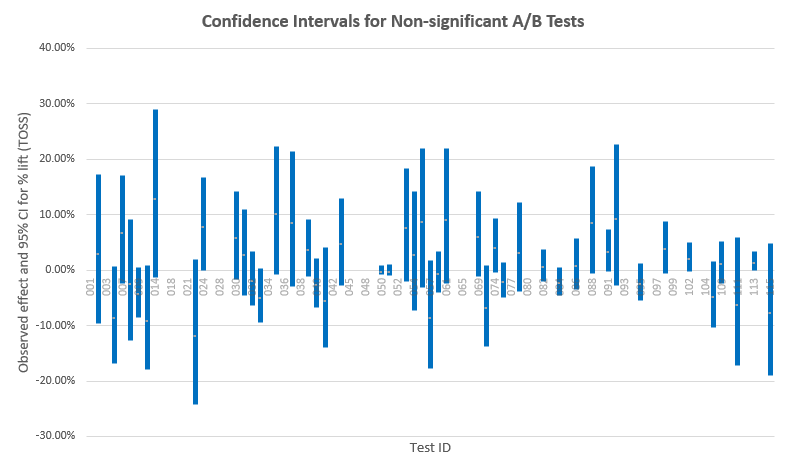

有一部分的测试有着围绕零点的狭窄区间，它们都是检定力良好的测试。当中几个更是正相等测试，即在这些测试中变量和对照之间很大机率没有任何差异。GoodUI并没有很好地利用这一点，而是粗略地把它们定义为”不显著”，而失去了能从这些数据中获取信息的机会。

留意有着负值观察结果的测试实际上也覆盖了大程度的正值效应，反之亦然，这些都是检定力低下的测试。一般来说，区间越宽，测试的检定力就越低下。

现在让我们检视一下统计上显著的测试的置信区间，从中我们能了解观察效应大小和真实效应大小的接近程度︰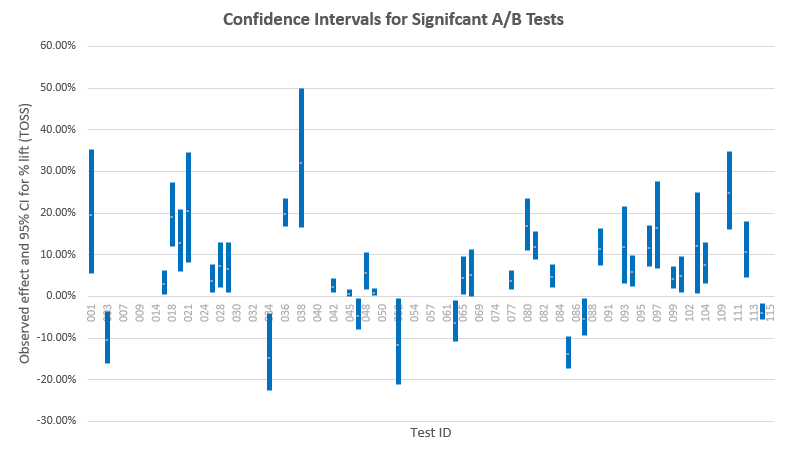

我们可以看到绝大部分测试几乎没有排除到0%附近的区域，很多区间只坐落在0%附近的几个百分点。如果笔者关于数据窥探的怀疑是正确的，那么这些测试的结果则相当有问题。某些区间颇为远离0%，说明它们的数据很大机会反映了实际情况中会出现很大程度的差异。

同样地我们能看到比较狭窄的区间来自检定力高的测试，而比较阔宽的区间则来自检定力低下的测试。举个例子，测试#36和#38都有着高于16%提升的下界，但测试#38的信赖区间较为阔宽，显出它是检定力低下的，而下界远离0%的原因来自较大的观察效应大小（也非常有可能是真实效应大小）。当然，以上假设的前提是测试中没有出现数据窥探和其他统计上的滥用问题。

讨论和重点

在115个测试中只有31个有着统计上显著的正值结果（在数据修剪后），这比起其他行业报告中如10%或5%的低数值来得要高。显著性结果的缺失部分是由于大约70%的测试经过分析都没有很好的检定力，另一方面则是因为测试中的干预不够有效，又或者没有造成明显的负值效应。而在考虑这些数字是否能代表行业情况时，也要考虑报导/出版的偏差。

关于统计上显著的正值测试，它们的平均百分比改变为10.73%（中位数7.91%）。这一结果在测试时长方面部分受挫于统计上显著的负值测试，原因是显著测试的平均值是6.78%（中位数5.96%），而全部测试小于4%（平均值3.77%，中位数3.92%）。笔者相信即使这一数据缺失了其代表性，它仍能帮助告知决策者有关转换率最优化程序的可能结果，笔者也相信它能在从业者决定是否把最小可检定效应放到检定力和样本大小计算中时起到帮助作用。笔者在做出这些决定时全凭每个独立A/B测试的水平，同时考虑到全部成本和回报，但外部基准在评估与测试有关的风险和回报时绝对有帮助。

而在研究测试时也有机会忽略有关在任何显著大小下的效应缺失的有力数据，原因在于相关测试被标签为”不显著”。

因为在元分析中的样本并不具代表性，所以得出的结果在用途上会有一定限制。另一个值得考虑的问题是测试有着不同的主要输出︰有的关注于改变轻微的点击行为，有的关注于改善试验注册，购买率，等等。

在报告中的测试没有一个以收入作为主要KPI的，而当中最少一个测试（#24）的主要输出与以收入为基本的KPI有着直接分歧（测试的成功有可能损害到中期和长期的收入）。还有一个问题是缺乏有关测试中用到的停止准则的信息︰如果以上提及的假设是正确的，而且有70%或更多的测试没有被正确地实行，那么一大部分的测试结果有可能是带有偏差的，且偏向任一方向的显著结果。

就A/B测试的收集和报告而言，笔者认为重点相当明显︰确保适当地计算统计量，而前提是需要知道测试在统计上是怎样设计的。需要知道测试是固定样本还是连续观察的设计，如果是连续观察的设计，那么分析的数目和时间又是多少。需要知道测试的变量数，又在人流分配中有没有任何值得怀疑的地方等等。这些都已经在之前的文章或者其他地方中讨论过。

原文标题︰

Analysis of 115 A/B Tests: Average Lift is 4%, Most Lack Statistical Power

译者简介：Gabriel Ng，清华大学概率统计方向本科生在读，一个热爱于数据分析和语言学习（和音乐）的THUer，平日活动离不开学习、健身和音乐。喜欢从数据探勘各类问题的本质，从语言认识不同文化的故事。希望通过学习和经验的累积，能以不同的角度，理性地分析问题，感性地认识问题。

转自：数据派THU 公众号；

END

合作请加QQ：365242293

数据分析（ID : ecshujufenxi ）互联网科技与数据圈自己的微信，也是WeMedia自媒体联盟成员之一，WeMedia联盟覆盖5000万人群。