「九章」刷屏的背后:万字长文解析,量子计算机和电子计算机各有何优劣?
机器之心转载
12月4日,中国科学技术大学潘建伟研究团队与中科院上海微系统所、国家并行计算机工程技术研究中心合作,成功构建了 76 个光子 100 个模式的高斯玻色取样量子计算原型机「九章」,其处理特定问题的速度比目前最快的超级计算机「富岳」快了一百万亿倍。相关论文登上了国际顶级期刊《Science》杂志,引发学界、业界热议。

这个机器非常简单,至少是在数学模型的意义上。
这个机器的输入的格式是有限的,这个机器可以执行的操作也是有限的。所以在现实中你可以用有限的零件制造它。
需要构成这个机器的基本操作都是非常简单的,而且只需要固定的时间就可以完成。
这个机器是万能的。只要你能够用逻辑和数学描述一个算法,它就能自动执行它。
这个机器是通用的,它可以模拟任何一种计算机器,包括它本身。
没有任何一种机器在使用算法解决问题上比它更加强大。如果一个问题它不能解决,那么其他机器也一定不能解决。

如何确定一个问题可以被图灵机解决。
如何设计算法。
如何将算法变成一堆符号。
如何制造图灵机一样的机器。


我们可以区分不同的状态。
我们有足够多的的状态
如果我们知道具体的状态,那么我们就可以将它改变为另外一个具体的状态。
在物理模型中找到一个基本的物理状态。确保这个物理状态可以通过组合产生任意大的状态。
利用物理模型的演化规则来实现
,从而可以控制状态。
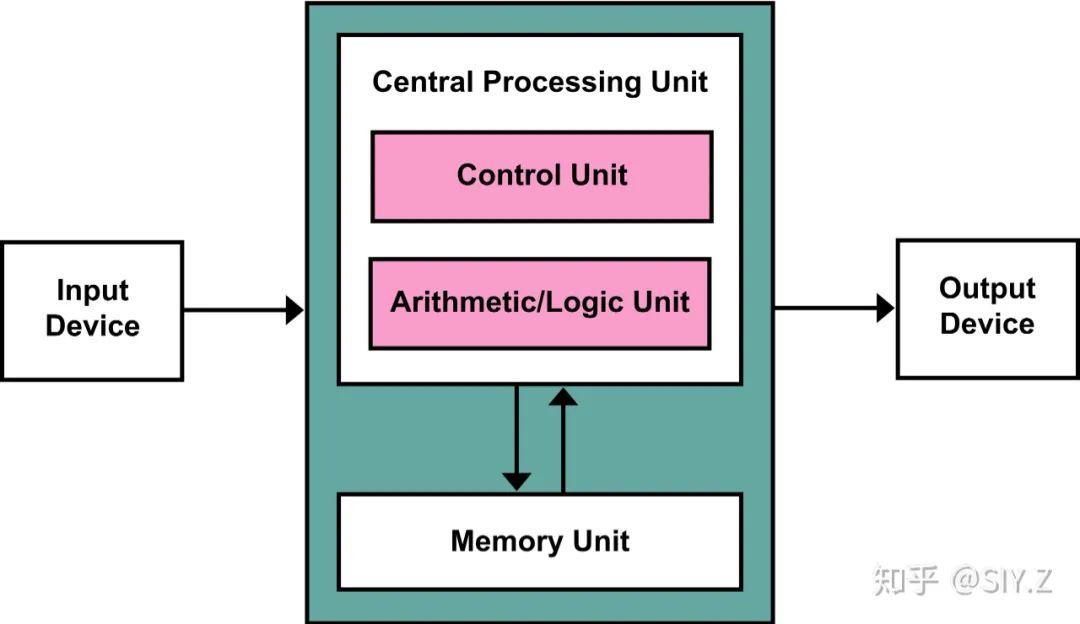
电子计算机使用电压表示状态,用固体物理的性质控制状态。
生物计算机使用 DNA 和其他化学物质表示状态,用酶和其他化学物质控制状态。
光学计算机使用光的性质表示状态,用光学元件控制状态。
量子计算机使用 “量子叠加态” 表示状态,用固体物理 / 光学元件 / 光学共振腔等控制状态。

(大邱奇-图灵论题)整个宇宙和一切物理过程都可以用图灵机模拟。
这个物理模型中,物理状态都是由向量而不是数表示。我们可以用固定的时间构造任何我们想要的任何元素个数的向量。
这个物理模型中,你可以用固定时间构造一个矩阵。这个世界遵循这样的物理演化规则:你可以用这个矩阵乘这个向量得到一个新的向量,这个新的向量就是新的物理状态。并且,这个操作用固定时间就可以完成(现实世界中需要和矩阵元素一样多次乘法操作)。
1、经典计算机中的任意一个状态,或者二进制串,都可以对应到一个向量:比如
这些都是正交的单位向量,且一个元素个数为的二进制串对应了一个元素个数为
的向量。有自然语言处理(NLP)经验的应该感到很熟悉,这其实就是 one-hot encoding。
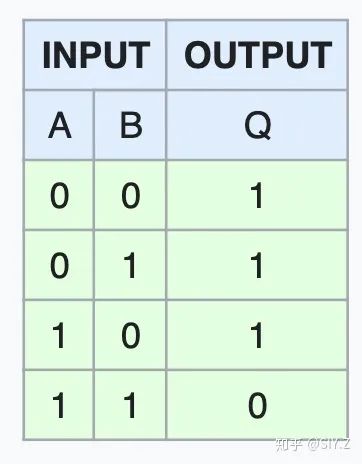
2、经典计算机中任意一个组合逻辑,都可以对应到一个矩阵。这个很显然,由于状态都是单位基向量,所以只要往矩阵对应的位置填上 1,就可以实现所有的功能。比如 NAND 对应的矩阵: 。
由于只有右下角有一个 1,所以只有作为列向量相乘才会输出
。用类似的方法可以表示任何一个组合逻辑。
物理状态的约束:量子态向量的模长固定为 1。也就是只有向量的方向是重要的,你无法使用它的 “长度” 做任何计算。
状态制备 / 初始状态的约束:我们仅能够使用
步准备一个元素个数为
的 one-hot 量子态。这一般作为算法的最初输入。one-hot 即整个向量中,只有一个系数是 1,其他均为 0。
演化的约束:从一个量子态到另一个量子态的演化对应的矩阵必须是幺正的(幺正演化),不改变向量的模长。也就是唯一可以对向量进行的操作是“旋转”。所有的幺正演化都是可逆的矩阵。
读出的约束:读出结果只能通过 “观测” 完成。根据量子力学的观测公理,一个算法输出的结果只能是一个 one-hot 量子态。得到某个 one-hot 量子态的概率为这个 one-hot 量子态在原来向量中的系数的平方(严格来说是模平方,因为系数可以是复数)。
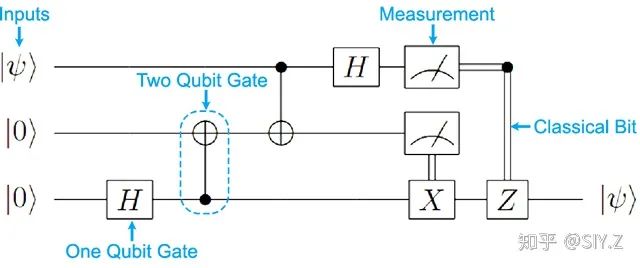
最直接的困难就是,不允许对未知的一个状态进行复制(比如说算法输入的某个量子态,以及所有受到输入影响的状态;这里要顺便指出量子图灵机中的 “读取” 和“写入”也不是通过复制完成的,而是通过 “交换“或者” 观测 “等量子力学允许的方式实现)。这是“量子不可克隆定理” 限定的,本质上是幺正操作和测量无法复制未知的状态。这让很多经典算法设计思想很难应用到量子算法设计上。
如何利用量子态的性质来加速也是一个问题,因为如果设计出来的算法没有明显超过经典算法,那么在解决问题上是没有意义的。如果使用经典的算法设计思想,是很难造出超过经典算法的量子算法的。
输入输出问题。如果输入输出是某个特定的 “量子态”,那么设计一些量子算法会变得相当容易,但是现实世界无法去直接利用量子态(因为量子力学根本上阻止我们直接观测它们)。因此如何从经典比特构造出想要的“量子态”,以及如何保证最终将“量子态” 通过观测变成想要的经典比特,是一个大麻烦。
通用量子计算机出现前,相关领域缺乏研究动力。
规模为
的快速傅立叶变换可以被
的矩阵乘法描述
快速傅立叶变换是可逆的,它的逆变换也是矩阵
快速傅立叶应用于向量不会改变向量的模长

已知 ,
和
是两个很大的质因数。已知
,求解
和
。
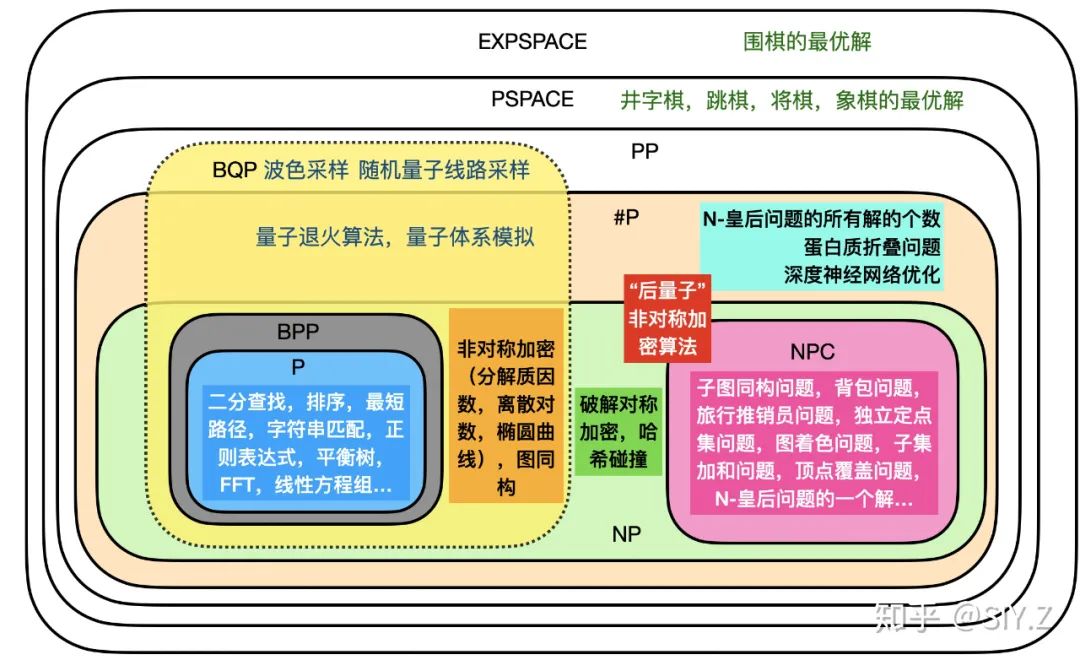
P ?= NP
P ?= BPP ?= NP ?= #P ?= PP ?= PSPACE




和 QFFT 一样,输入的向量必须编码到是量子态向量的系数上。如果向量最初是经典计算机中的向量,那么显然读取数据就需要
步(因为向量本身有
个元素),这样你就无法获得加速优势。同样的,矩阵本身的元素也不能全部来自经典计算机的稀疏矩阵,否则读取数据就会占用更多时间。所以大部分机器学习问题,除非人为构造数据,否则很难直接用 HHL 加速。
矩阵必须是稀疏的,也就是
远小于
,否则主导运行时间的就是
,而不是
,加速效果就会大打折扣。完全无视这一点的相关研究可以说几乎是故意在骗人了。当然,也有一个 HHL 的变种算法,可以加速稠密的线性方程组的求解,但是相对经典算法并没有指数加速。
输入的稀疏矩阵必须是可逆的,而且数值特性良好,否则状态数
会很大,这样也会失去加速。
这个算法的输出和输入一样,也是编码到量子态向量的系数上的,这意味着你没有办法直接将结果直接转换成经典的表示,比如导出成一个数组,打印到屏幕上。不过,你可以通过一些后续的算法研究这种输出的一些性质(虽然还是不能直接得到输出)。
如果你的问题没有上述任何一个困扰,那么恭喜你,你可以使用 HHL 来指数加速你的问题求解。

© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/
 关注网络尖刀微信公众号
关注网络尖刀微信公众号随时掌握互联网精彩
- 1 习近平同马克龙交流互动的经典瞬间 7904750
- 2 日本飞机多次抵近滋扰中国海军训练 7808048
- 3 荷兰大臣:没想到中方叫停芯片出口 7713695
- 4 三项世界级成就见证中国实力 7618715
- 5 苏州地铁全网寻找用围巾擦地女孩 7522590
- 6 70岁老太西安城墙上模仿士兵走位 7423868
- 7 公考枪手替考89次敛财千万 7330497
- 8 为让婚车不走回头路司机放倒三轮车 7233519
- 9 危险信号!俄数百辆保时捷突然被锁死 7141850
- 10 今日大雪 要做这些事 7041639







 机器之心
机器之心







