推荐 :用归纳偏置来增强你的模型性能
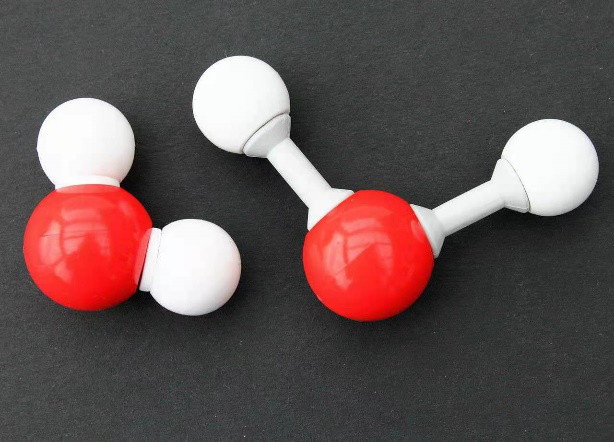

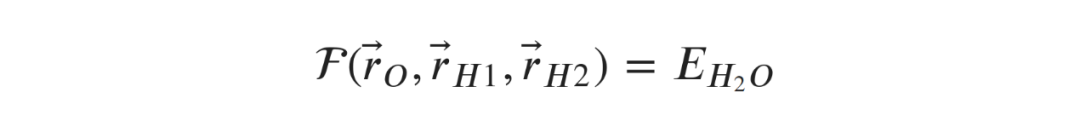


在化学和物理应用机器学习的早期,研究者很快意识到模型需要观察这些对称性才能足够精确。因此,人们投入了大量的精力来研究如何在机器学习算法体现出对称性。现在,这通常是通过巧妙的特征工程和神经网络设计相结合来实现的。关于这些方法的全面评述可以在这里(https://aip.scitation.org/doi/full/10.1063/1.4966192)找到[1]。所有这些方法都有一个共同点,就是它们以某种形式向学习算法引入了归纳偏置。
线性回归是基于因变量与协变量之间存在线性关系的假设。
k近邻分类器假设特征空间中的邻近转换为输出空间中的邻近。
卷积神经网络假设输出在很大程度上不受输入转换的影响(不考虑边界条件)。
单元类型:零售,办公,生活空间
单元面积:以平方英尺为单位
房间数量
窗户与墙壁的比率
单元在哪一层(以楼层总数的比率给出)
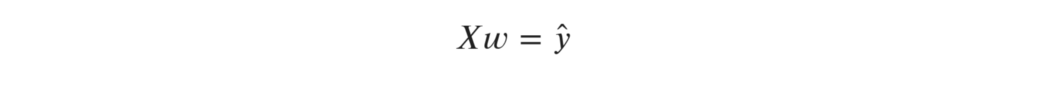
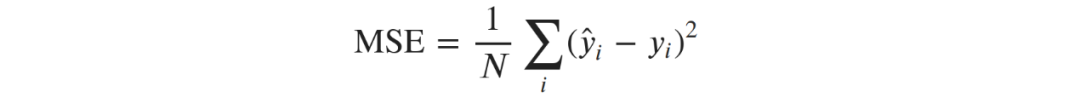
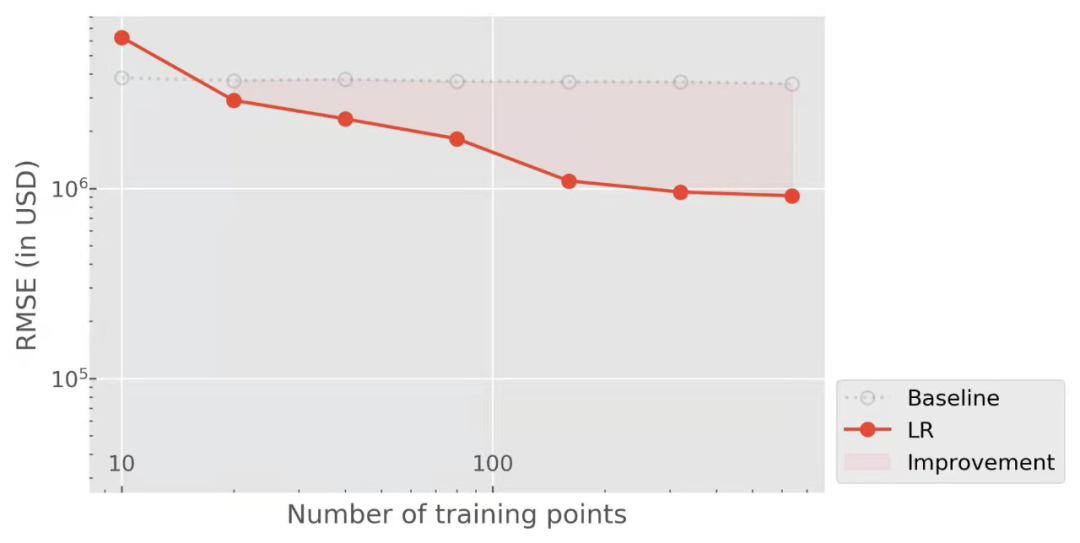
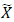 。考虑每单元(每5列一组)作为一个单独的数据点,矩阵原始X转化后维数为10000a?5由。线性回归则为
。考虑每单元(每5列一组)作为一个单独的数据点,矩阵原始X转化后维数为10000a?5由。线性回归则为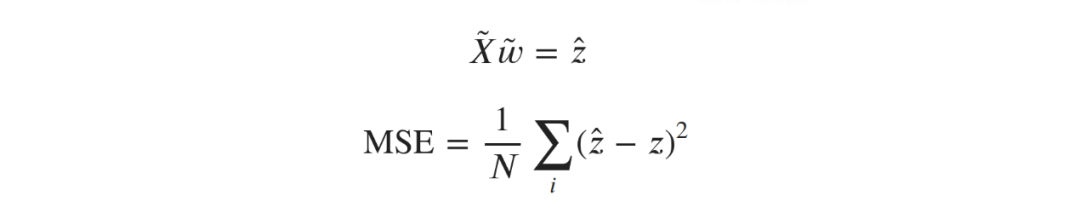
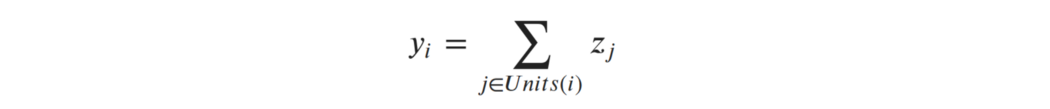
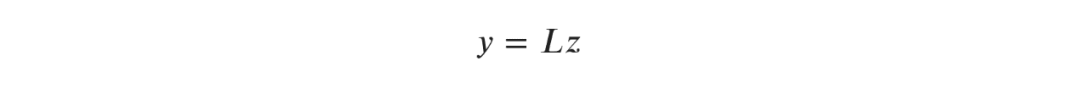

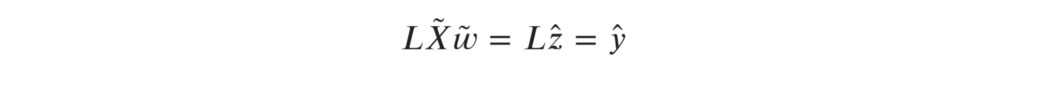
 意味着我们总结一个建筑所有单元的特征,所以我们只使用建筑总面积而不是每个单元的面积。所以对于线性回归来说,强加排列对称真的是一个微不足道的任务。当我们转到内核方法时,使用这种更抽象的表示法的优势将变得清晰起来。
意味着我们总结一个建筑所有单元的特征,所以我们只使用建筑总面积而不是每个单元的面积。所以对于线性回归来说,强加排列对称真的是一个微不足道的任务。当我们转到内核方法时,使用这种更抽象的表示法的优势将变得清晰起来。
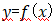 映射输入,或自变量x对因变量y(价格)。在高斯过程回归中,我们用贝叶斯方法先找到这个函数,即首先在所有可能的f上指定一个高斯先验分布,然后对观测数据点(X,y)进行条件处理(即基于先验和一定的假设(联合高斯分布)计算得到高斯过程后验分布的均值和协方差。)。这个先验通过协方差矩阵为k的高斯过程定义:
映射输入,或自变量x对因变量y(价格)。在高斯过程回归中,我们用贝叶斯方法先找到这个函数,即首先在所有可能的f上指定一个高斯先验分布,然后对观测数据点(X,y)进行条件处理(即基于先验和一定的假设(联合高斯分布)计算得到高斯过程后验分布的均值和协方差。)。这个先验通过协方差矩阵为k的高斯过程定义: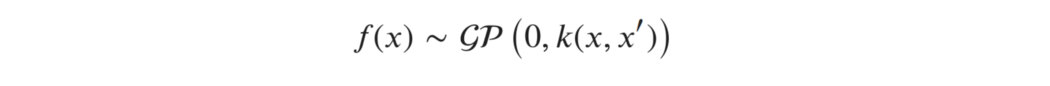
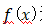 遵循正态分布。进一步,两个距离较远的点x和x’点的输出在在定义为
遵循正态分布。进一步,两个距离较远的点x和x’点的输出在在定义为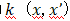 的协方差条件下是联合正态分布的。在实践中,这意味着我们可以通过选择一个合适的协方差函数(也称为核)
的协方差条件下是联合正态分布的。在实践中,这意味着我们可以通过选择一个合适的协方差函数(也称为核)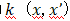 来确定拟合函数f的形状。
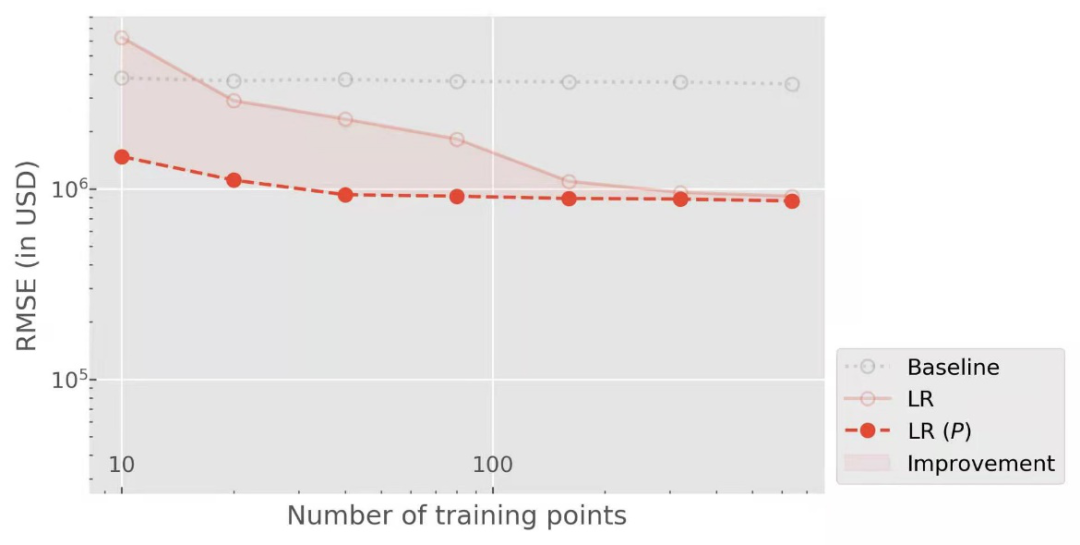
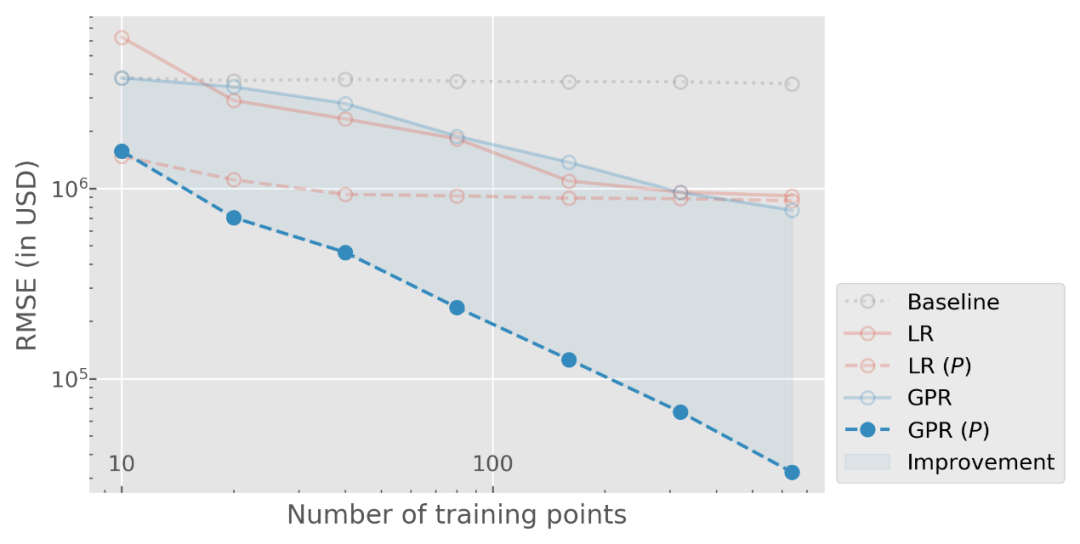
来确定拟合函数f的形状。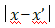 很小),点之间将是高度相关的。让我们回到我们的例子。一旦我们在训练数据上设定高斯过程的条件,我们就可以在测试集上做出预测。
很小),点之间将是高度相关的。让我们回到我们的例子。一旦我们在训练数据上设定高斯过程的条件,我们就可以在测试集上做出预测。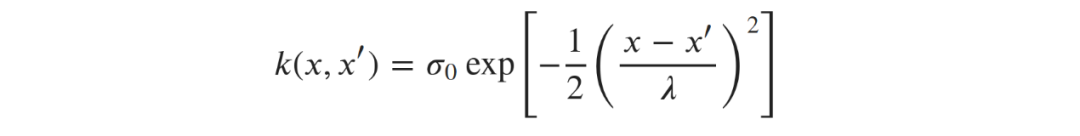
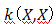 已经取代了X。因为w的参数方程是线性的,它仍然是直接可解的:
已经取代了X。因为w的参数方程是线性的,它仍然是直接可解的: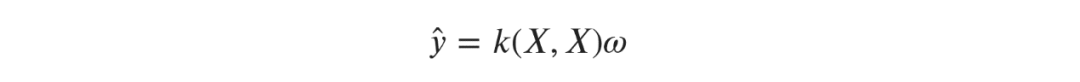
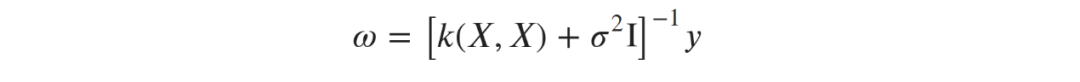
 并乘以单位矩阵。该参数用于拟合数据中的噪声,同时有助于避免矩阵求逆时的数值问题。
并乘以单位矩阵。该参数用于拟合数据中的噪声,同时有助于避免矩阵求逆时的数值问题。
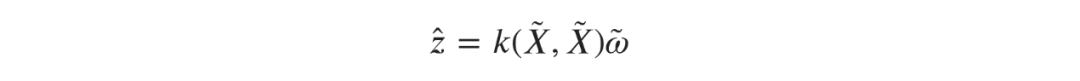
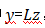 ,矩阵L与线性回归问题中相同。
,矩阵L与线性回归问题中相同。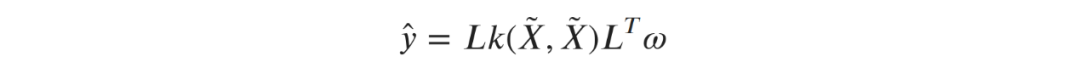
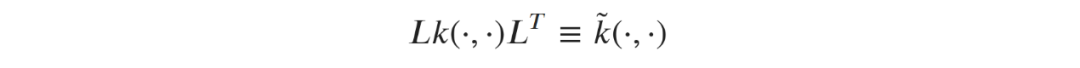
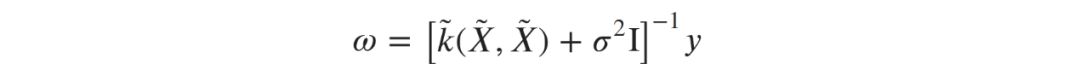
[1] Behler, J?rg. “Perspective: Machine learning potentials for atomistic simulations.” The Journal of chemical physics 145.17 (2016): 170901.
[2] https://en.wikipedia.org/wiki/Inductive_bias
[3] C. Cortes, L. D. Jackel, S. A. Solla, V. Vapnik, and J. S. Denker, Learning Curves: Asymptotic Values and Rate of Convergence, Advances in Neural Information Processing Systems (Curran Associates, Inc., 1994),
pp. 327–334
[4] C. E. Rasmussen & C. K. I. Williams, Gaussian Processes for Machine Learning, the MIT Press, 2006, ISBN 026218253X. c 2006 Massachusetts Institute of Technology
[5] Bartók, Albert P., et al. “Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons.” Physical review letters 104.13 (2010): 136403.
原文标题:
Supercharge your model performance with inductive bias
原文链接:?
https://towardsdatascience.com/supercharge-your-model-performance-with-inductive-bias-48559dba5133
译者简介:车前子,北大医学部,流行病与卫生统计专业博二在读。从临床医学半路出家到数据挖掘,感到了数据分析的艰深和魅力。即使不做医生,也希望用数据为医疗健康做一点点贡献。
END
转自:?数据派THU 公众号;
版权声明:本号内容部分来自互联网,转载请注明原文链接和作者,如有侵权或出处有误请和我们联系。
合作请加QQ:365242293??
数据分析(ID?:?ecshujufenxi?)互联网科技与数据圈自己的微信,也是WeMedia自媒体联盟成员之一,WeMedia联盟覆盖5000万人群。

关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/
 关注网络尖刀微信公众号
关注网络尖刀微信公众号随时掌握互联网精彩
- 1 从五年规划看“中国之治” 7904462
- 2 中俄轰炸机航母3个方向“包围琉球” 7808197
- 3 为一棵树拨打12345 引百万网友围观 7713658
- 4 长征系列火箭一日三发 7616949
- 5 上海出现“地震云”?气象专家回应 7523126
- 6 男子飞无人机在崖洞发现干尸 7426224
- 7 高市早苗承认中日关系恶化冲击经济 7328979
- 8 央视马年春晚官宣 7237532
- 9 71岁成龙回应“龙叔老了” 7139325
- 10 冷空气南下 这些地方流感风险上升 7040171







 数据分析
数据分析







