蝴蝶扇了一下翅膀，混沌就诞生了

你是否曾经想过什么是混沌理论？

给我几分钟，我将给你介绍理论物理中我最喜欢领域之一的基础知识，以及这理论所展现的精美图像——而这只需要加法和乘法就可以达成这个效果，准备好被震惊吧！

在上世纪六十年代初期，麻省理工学院的教授爱德华·洛伦兹致力于利用大学里面最新的大型计算机来预测天气。他推导出了描述空气对流的一组简单方程，并利用计算机来求解这个方程。

接下来发生的事情使他大吃一惊：在没有任何随机数引入的情况下（确定系统），计算机利用同样参数两次跑出的结果大相径庭。混沌理论被发现了！

所以，洛伦兹的天气预测中，发生了什么？看下面这个例子。

这当然是一个确定系统，完全没有随机数的引入。

现在，我的问题来了：你能预测这些数字的未来发展状态么？

答案是“既能也不能”。对于更多有限的步骤，可以得出很准确的答案。但是，100步之后呢？题目并没有给出足够的位数。计算机存储小数点之后的位数是固定的（取决于你数字的类型）。一个64位的双精度数有16位十进制的数字，所以，在进行上述的操作15次之后，你将无法获得预测的结果。如果你会编程，我建议你自己尝试一下！在早期的计算机中，这样的方程甚至被用作伪随机数的生成器。

就算我们知道小数点之后的100或者1000位，在此之后，结果都是不可预测的，因为在每次操作中，由于删除了小数点之前的数，破坏了信息。因此最后得到的结果，尤其依赖于初始条件。

到这里为止，我们先总结一下我们已经得到的结论：

混沌方程是确定性的方程或者系统（代表没有随机数参与，且明确计算当前态到未来态的结构），同时非常依赖于初始条件，使得我们不可能预测长远的未来。

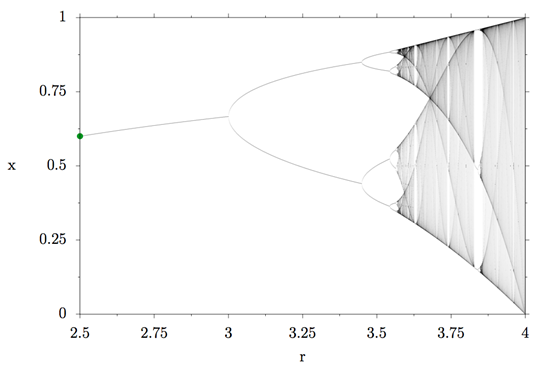
本文开始的图片是所谓的逻辑图的分叉图的放大区域（如下图）。读完这篇文章之后，你将明白如何解释这幅图，这也是整个物理领域中我最喜欢的图之一:)

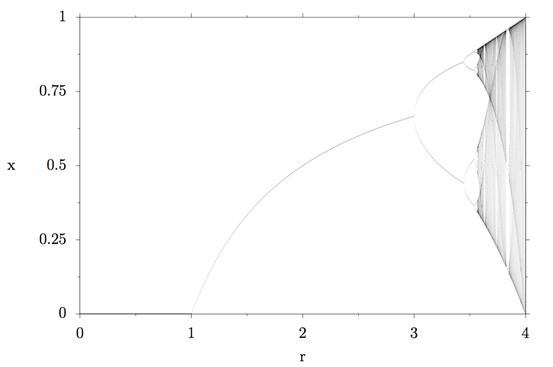
逻辑图的分叉图

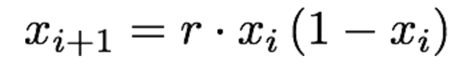
这是逻辑图的方程。别担心，让我们一起看看一下这个方程表示了什么。

逻辑图描述了种群数目模型，该模型包含两个控制种群规模的对抗部分：种群的繁衍和由于食物供应有限导致的死亡。如果种群中没有生命，x就是0；x=1代表着种群已经到达了最大值（由于食物有限），r是繁衍率。

下标i代表在时间i时的种群数目，下标i+1代表下一个时间的种群数目。这代表着，如果我们知道现在这个时间的种群数目以及繁衍率，就可以计算下一个时间的种群数目。

可以举一个简单的例子。简单起见，假设繁衍率r=1，假如种群初始数目为最大数目的80%，即x₀=0.8。

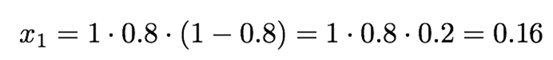
这代表着种群从最大可能种群的80%缩减到16%。原因是种群没有繁殖出足够的数量，也没有足够的食物来维持现有的x=0.8种群。

方程中的 “1×0.8”代表出生的人口。繁衍率越高，出生数目就越多。这里我们把繁衍率取为1，因此下一步中结果仍为0.8；

“1-0.8”部分代表因饥饿导致的死亡。“r·x₀=1×0.8” 这一项乘以系数“1-0.8=0.2”，代表5个生物中有4个饿死了。x的值越接近1，越多的生物会死亡。（幸好，这只是模型。）

那么照这样下去这些会怎么发展呢？下面的图展示了种群随时间发展的趋势。图中发生了什么呢？种群x趋于0，代表生物的出生率小于死亡率，因此最终会灭绝。

回到分叉图中，我们用黑点表示x=0，繁衍率r=1，如下图所示。

繁衍率在0~1之间的种群会灭绝

对于更大的繁衍率的种群，比如说r=2.5：

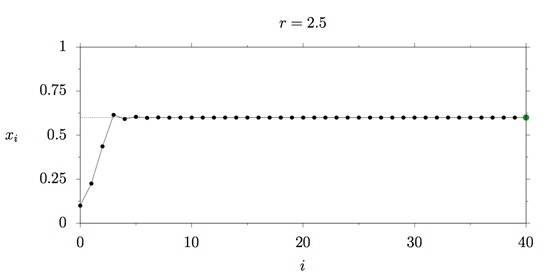
种群的大小快速达到了最大可容纳值的60%，然后保持不变，这被称为系统的不动点。不动点不依赖于x的初始值，只依赖于繁衍率r。在分叉图中，我们用绿色的点标示r=2.5和x=0.6，如下图所示。

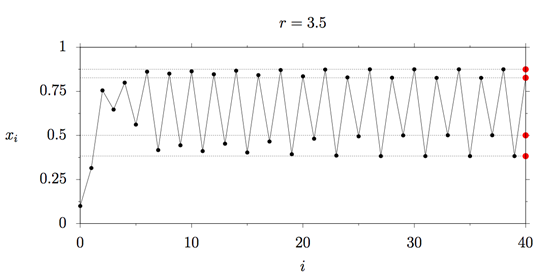
接下来我们把繁衍率提升到 r=3.25，看一看会发生什么。下图显示了种群发展的情况：你会发现种群会在两类种群规模之间震荡！

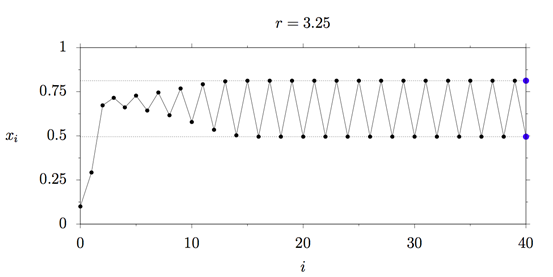
为什么会这样呢？在较大的种群规模下，我们模型中的所有生物都没有足够的食物，一些生物会因此死去，然后剩下的生物就会有足够的食物生存。但是一旦繁衍率再次提升，食物又会缺失，一些生物又会死去，这个过程不断循环……

在绿色的点的位置图像分为了两部分，物理学家称之为：倍周期。在分叉图中用两个蓝色的点标记r=3.25。

如果将繁衍率再度提升，你猜会发生什么？两个蓝色的点分裂为了四个，现在种群的数量在四个点之间振荡。

在分叉图中标记如下。

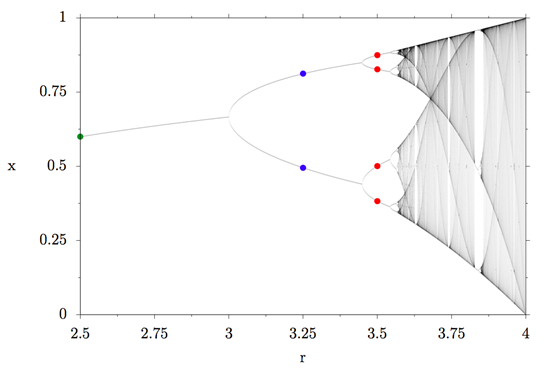
我们观察到的现象被称为：倍周期级联。4 个固定点成为了8个，8个变为16、32、64直至无穷大，在倍周期级联的最后，混沌就出现了。

在分叉图中，整个区域不用振荡的离散固定点表示，而是用灰色的区域表示，是因为这些点在这些区域都出现过，颜色越深，出现的次数越多。

如果观察 r=3.75的部分，可以看出，灰色区域从x=0.25左右开始，在x=0.9左右结束，代表种群数目在这些值之间不断变化。

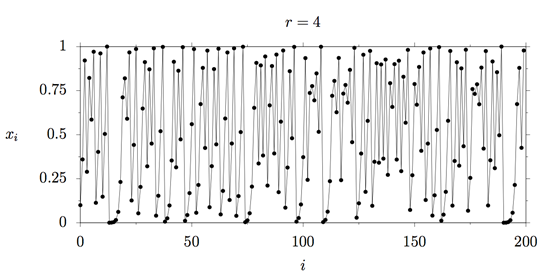
下图表示种群在r=4时的情况：种群的数目变化是完全混乱的。如果可以用数字多次计算这个趋势变化，你会发现：初始值的微小变化（由于数值精度的限制）会产生截然不同的结果，这就是混沌的主要特征。

到目前为止，一切还好。但是如果仔细观察混沌区域，会发现灰色区域中间有白色的条纹。这代表什么？让我们放大这个区域，仔细观察。

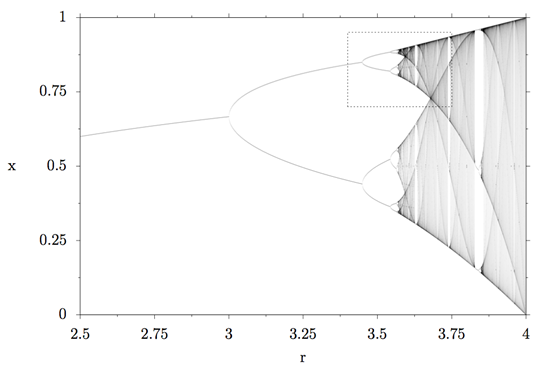
这看起来跟之前的图像非常相似，让我们放大第二个矩形。

你看见了什么？在r≈3.625的左边，只有混沌出现。在灰色区域，种群数目可以是灰色区域的任意值。然后，混沌突然消失，一个固定点出现了，这些白色的区域被称为稳定岛。然后同样的事情发生了，倍周期出现、二级倍周期……倍周期级联，混沌出现。

如果进一步放大，同样的事情出现：混沌区域的稳定岛、倍周期级联、混沌出现。再放大，更多稳定岛、倍周期级联、混沌……

我第一次学到这个的时候，这个现象绝对震惊到了我，纵使几年后亦然如此。所有这些复杂的混沌行为都能利用一个简单的模型来描述。

我尝试创建一个自相似的动画来展示这个现象，请着重注意闪烁的白色稳定岛和随处可见的倍周期级联现象。

有许多其他的混沌图展示了同样的现象，比如说如下面动画展示的高斯图（有时也被称为老鼠图，你能猜出原因么？）

这个图我们就不放大看了。图的方程包含了一项新的元素：α，在动画中α的取值是从3.5到8。

当曲线不断分裂成2、4、8……时，注意到会有周期倍增的现象。你能观察到在混沌区域出现的稳定岛和倍周期级联等所有元素。

关于混沌现象还有很多其他的图像，感兴趣的朋友可以戳下面的图片↓

蜘蛛网

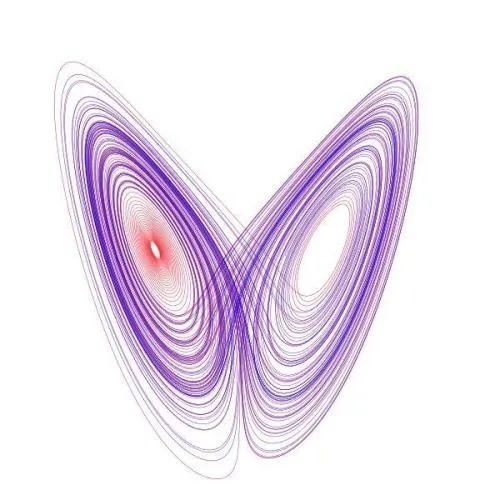
洛伦兹吸引子

有兴趣的读者们还可以自己动手编码画出属于自己的混沌图哦~