本文长度为2500字,建议阅读7分钟
这篇文章主要带大家入门PCA,逐渐理解PCA最原始的概念和设计思路,以及简单的实现原理。
主成分分析,即Principle Component Analysis (PCA),是一种传统的统计学方法,被机器学习领域引入后,通常被认为是一种特殊的非监督学习算法,其可以对复杂或多变量的数据做预处理,以减少次要变量,便于进一步使用精简后的主要变量进行数学建模和统计学模型的训练,所以PCA又被称为主变量分析。
朱小明买了五个西瓜,每个西瓜都有重量、颜色、形状、纹路、气味五种属性:注:这里的离散属性我们已经做了某种数字化处理,比如颜色数值越小表示越接近浅黄色,颜色数值越大越接近深绿色,形状数值越接近1代表越接近球形等。朱小明回到家,观察了西瓜们的五种属性,他觉得对于这五个西瓜来说,气味和形状是完全没有必要去关注的,可以直接丢弃不看。为什么?对于西瓜的重量属性和形状属性,我们发现这俩种似乎是不同的两种性质。把西瓜们的重量x和形状属性y拿出来画图示意:?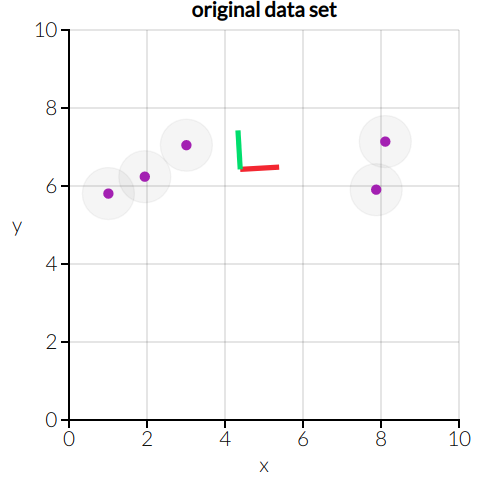
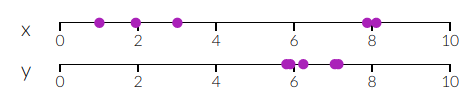
我们从数据分布上估计,相比x属性来说,y属性的方差(variance)不大,即所有的西瓜这个属性都不怎么变化。因此比较所有的西瓜时其实不用考虑y这一属性(反正所有西瓜的y属性数值都差不多相同,所以就不用关注了)。在数据科学和统计应用中,通常需要对含有多个变量的数据进行观测,收集后进行分析然后寻找规律,从而建模分析或者预测。多变量的大数据集固然不错,但是也在一定程度上增加了数据采集的工作量和问题分析和建立模型的复杂性。因此需要找到一种合理的方法,在减少需要分析的指标(即所谓的降维),以及尽量减少降维带来的信息损失,达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。上面举的西瓜的例子过于简单,显然形状和气味的属性差异太小,可以直接舍弃。但更一般的情形是某一些属性的线性组合才会差异太小,如果要降低维度,消减多余的属性,我们必须要找到这种组合。(实际生活中,很多变量中可能存在两种变量线性相关,造成信息冗余,实际上我们可以舍弃其中一种变量,在这里就表现为当存在某两种属性的数值其线性组合接近0时可以舍弃其中一个变量)以下图为例,有两个属性x,y的样本徘徊在一条直线附近。我们总是认为属性差异(variance)最大的情况下样本蕴含最丰富的信息,反之亦然。因此,我们会把特征空间里的base(坐标轴,下图中的黑色直线)重新选取并把base的数量由2减少到1,选择让这些点在新base下的信息最大。新base下的新样本就是一条直线上的点(红色的点),他们只有一个属性,一个维度。下图所示,我们总是有两种选择(我们真的只有这两种吗?的确有更多的选择,不过就不是PCA而是其他的降维算法了):找到新的base,使得样本点们到base的投影点们在新base下的分布数值方差最大,差异最大即信息最多,
找到新的base,使得样本点们到base的投影距离平方和最小,都很小那丢弃后损失的信息就少了。
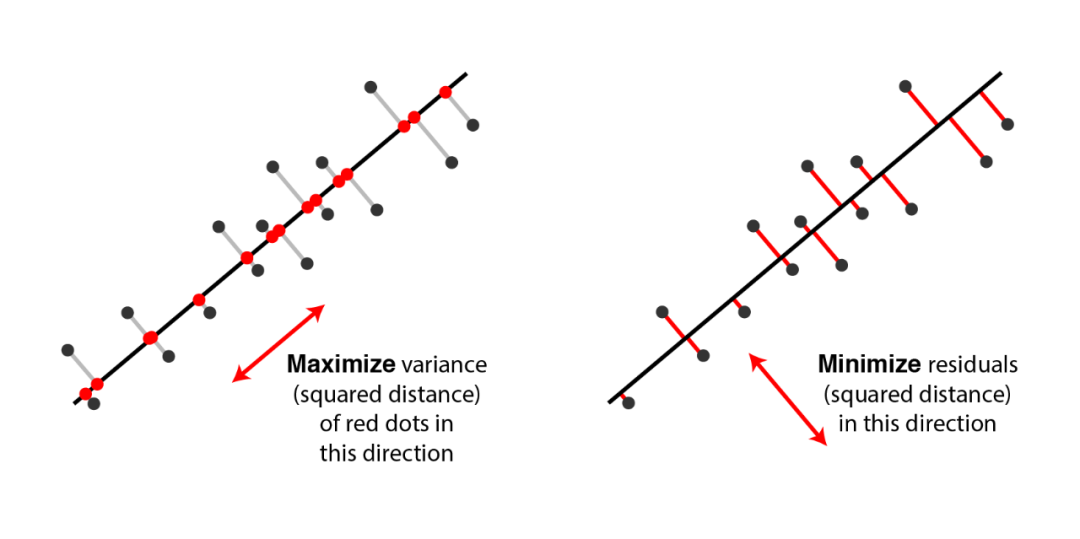
但实际上可以证明:这两种方法是等价的。(先思考一下这是为什么?)数据集记为,若简单假设每个样本具有两个属性,容易知道,所有样本的属性构成了一个均值为的分布,该分布具有自己的均值和方差。但假如我们事先对数据集做了去中心化的预处理,即所有属性都减去了它们的均值,则这里有预处理后的特征的方差应为。我们这时要寻找一条新的base: 使得所有:在的新base:上的投影后数值分布的方差最大。1)投影不会改变分布的均值,所以投影后的均值依然为0,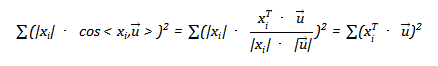
最大,而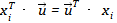 ,因此等价变换后要使得
,因此等价变换后要使得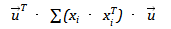 最大,记该最大值为
最大,记该最大值为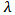 。(事实上,样本的协方差矩阵很像这个矩阵,这个矩阵是半正定的,其特征值均不小于0)?
。(事实上,样本的协方差矩阵很像这个矩阵,这个矩阵是半正定的,其特征值均不小于0)?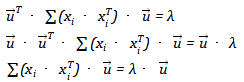
这里把类似协方差矩阵的这一坨记为矩阵,那么此时就变成了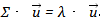 。即需要求解矩阵的特征向量。所以的最大值也就是矩阵最大的特征值,而此时的新base
。即需要求解矩阵的特征向量。所以的最大值也就是矩阵最大的特征值,而此时的新base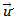 也就是最大特征值对应的特征向量。一句话概括,要对一批样本进行降维,需要先对所有的属性进行归一化的减均值处理,然后求其协方差矩阵的特征向量,将特征值按从大到小的顺序排列,特征值越大的新基对应的新样本属性就越重要。最后我们就可以按照需要舍弃最后面特征值较小对应的特征向量作为新基下投影的样本属性了。Not finish! We need to think more!1.最开始的时候,我们假设样本点中线性组合后的一些属性可能方差就变成0了,那我们就可以扔掉这些属性,但是如果这些属性必须经过非线性组合之后,方差才可能变成0,我们应该怎么发现这种组合并加以选择行的丢弃呢?比如我们有以下样本点(7.3, 1.6, 8.1) ,(5.2, 9.7, 0.6) ,(6.8,3,8.1) ,(1.7,9.6,5.2) ,(3.7,8.9,5.4),我们可以把这三个维度降低到几维还能保持90%以上的方差呢??(提示:kernel PCA,答案是可以降低到1维)
也就是最大特征值对应的特征向量。一句话概括,要对一批样本进行降维,需要先对所有的属性进行归一化的减均值处理,然后求其协方差矩阵的特征向量,将特征值按从大到小的顺序排列,特征值越大的新基对应的新样本属性就越重要。最后我们就可以按照需要舍弃最后面特征值较小对应的特征向量作为新基下投影的样本属性了。Not finish! We need to think more!1.最开始的时候,我们假设样本点中线性组合后的一些属性可能方差就变成0了,那我们就可以扔掉这些属性,但是如果这些属性必须经过非线性组合之后,方差才可能变成0,我们应该怎么发现这种组合并加以选择行的丢弃呢?比如我们有以下样本点(7.3, 1.6, 8.1) ,(5.2, 9.7, 0.6) ,(6.8,3,8.1) ,(1.7,9.6,5.2) ,(3.7,8.9,5.4),我们可以把这三个维度降低到几维还能保持90%以上的方差呢??(提示:kernel PCA,答案是可以降低到1维)
2.我们可以用求新基下投影距离平方和最小值的方式推导吗?3.协方差矩阵为什么会出现?回想一下协方差矩阵在统计学中的含义是什么?因为方差是一些平方和,所以肯定不是负的,那么轻易可以得到协方差矩阵的特征值一定不为负。那实际用matlab或者python计算的时候为什么还会出现特征值是负数的情况呢?(SVD浮出身影)4.听小朋友说t-SNE也是一种降维方法,通常用于高维空间到低维空间的可视化分析。那么这里的t-SNE采用的是PCA的方法吗?(不是)本文主要简单介绍了PCA的原理和思想,但更多相关知识比如计算的稳定性、如何加速计算、遇到庞大的稀疏矩阵如何处理等并未涉及,希望大家能举一反三,积极思考,自学成才。A word to finish: PCA虽然好,但也不是万能的。优点:无监督学习,根本不需要样本的标签信息;PCA后所有主成分正交,再无信息冗余之忧;计算简单。缺点:解释性不佳(比如:PCA后发现西瓜最重要的属性是0.3×颜色+0.7×重量。这是什么属性??);某些特殊情况下方差小的属性未必信息无用,方差最大化未必就一定信息最大。参考资料:
http://setosa.io/ev/principal-component-analysis/END
转自:?数据派THU 公众号;
版权声明:本号内容部分来自互联网,转载请注明原文链接和作者,如有侵权或出处有误请和我们联系。
合作请加QQ:365242293??
数据分析(ID?:?ecshujufenxi?)互联网科技与数据圈自己的微信,也是WeMedia自媒体联盟成员之一,WeMedia联盟覆盖5000万人群。
关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/



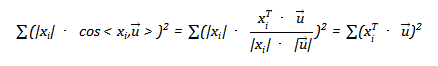
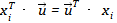 ,因此等价变换后要使得
,因此等价变换后要使得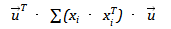 最大,记该最大值为
最大,记该最大值为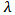 。(事实上,样本的协方差矩阵很像这个矩阵,这个矩阵是半正定的,其特征值均不小于0)?
。(事实上,样本的协方差矩阵很像这个矩阵,这个矩阵是半正定的,其特征值均不小于0)?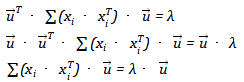
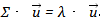 。即需要求解矩阵的特征向量。所以的最大值也就是矩阵最大的特征值,而此时的新base
。即需要求解矩阵的特征向量。所以的最大值也就是矩阵最大的特征值,而此时的新base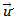 也就是最大特征值对应的特征向量。
也就是最大特征值对应的特征向量。
 关注网络尖刀微信公众号
关注网络尖刀微信公众号






 数据分析
数据分析







