
导语:深度学习领域经典的 Adam 算法在大规模并行训练的情况下会导致模型性能损失。为了解决这一问题,微软亚洲研究院采用 BMUF 框架对 Adam 算法进行了并行化,并在微软大规模 OCR 和语音产品数据集上进行了测试,使其在并行训练中几乎实现了线性加速的同时,模型性能基本无损。来源 | 微软研究院AI头条(ID: MSRAsia)作为一种自适应步长随机梯度优化器,自2014年提出以来,Adam 算法便以其卓越的性能风靡深度学习领域。为了提高应用于训练大规模任务时的效率,该算法通常与同步随机梯度(Synchronous Stochastic Gradient,SSG)技术相结合,采用数据并行(data parallel)的方式在多台机器上执行。在本文中,我们称这一方法为 Sync-Adam。本质上来讲,Sync-Adam 通过将一个 minibatch 内样本的梯度计算分布到多台机器上达到加速目的,因此通信十分频繁,并且随着并行机器数目增多,minibatch 内样本的数量也成比例增加,这种情况下,通常会损害最终得到的模型的性能。为解决基于 SSG 的 Adam 算法可扩展性差的难题,我们把目光投向了逐区块模型更新滤波(Blockwise Model-Update Filtering, BMUF)框架。BMUF 是一种通信高效的通用分布式优化算法框架,于2016年由微软亚洲研究院语音组的研究人员提出并发表。该算法在多个并行工作机之间周期性同步模型更新信息,并与历史更新信息相结合提升全局模型性能。与基于 SSG 的算法相比,BMUF 具有通信频率较低、训练几乎线性加速、模型性能基本无损的特点。这一算法已经在工业界广泛用于大规模深度学习模型的训练。本文中,我们采用 BMUF 框架并行化 Adam 算法,并在微软大规模 OCR 和语音产品数据集上进行了测试。实验结果表明,在大规模 OCR 任务中,BMUF-Adam 在多达64机的并行训练中几乎实现了线性加速的同时,基本没有模型性能损失,在32机大词汇量连续语音识别任务中也获得了类似效果。接下来我们探讨如何采用 BMUF 框架赋能 Adam 算法,在大规模深度学习任务上成就不凡。
在基于 BMUF 的训练框架下,假设我们总共有 N 个并行工作机,一个工作机可以是一块或多块 GPU 卡,也可以是一个计算节点。给定一个包含 Nτ 个 minibatch 的训练数据子集,首先我们将这些数据均匀分布到 N 个并行工作机,每台工作机获得?τ?个 minibatch。从一个共同的初始模型?θ_(t-τ)^((init)) 开始,N 个工作机独立更新各自的局部模型?τ?步,得到 {θ_(t,1),θ_(t,2),…,θ_(t,N)},对局部模型取平均得到 θ ?_t。这一过程称之为数据块内并行优化(Intra-Block Parallel Optimization, IBPO)。与直接将 θ ?_t 作为全局模型不同,BMUF 技术将历史更新信息与当前更新信息结合,得到全局模型:其中 η 是区块冲量(block momentum),ζ 为区块学习率(block learning rate),在本文中,我们设置 ζ=1。BMUF 通过采用区块冲量的方式弥补每个 minibatch 由于平均操作带来的对最终模型贡献不足的问题,来提升模型性能。为了方便接下来的分析,我们引入一个新的变量 ρ_n 表示 Δ_n 的等效 minibatch 数目,由于依据文献[2], 如果我们设置 η=1-1/N,那么 lim┬(n→∞)(ρ_n)=Nτ。通过这一推导可以看出,lim┬(n→∞)(Δ_n) 可以模拟序列化处理 Nτ 个 minibatch 的模型更新。上述的推导基于 θ ?_t-θ_(t-τ)^((init)) 的平稳性假设。本文中,我们采用 Nesterov 区块冲量技术,得到下一 IBPO 操作的初始模型:Adam 是一种采用随机梯度的一阶矩和二阶矩估计确定每个参数更新步长的算法,其具体形式如下:其中 θ_t 为模型参数,? 表示逐元素乘法,g_t 为第 t 个 minibatch 对应的随机梯度。在实际使用中,精确的一阶矩和二阶矩的获得需要大量的计算,Adam 算法基于 E[g_t] 和 E[g_t⊙g_t] 的短时平稳假设,采用随机梯度序列的指数滑动平均来对一阶矩和二阶矩进行近似:

由于 BMUF 是通用分布式优化框架,因此我们可以把 Adam 作为局部优化器嵌入其中。结合我们对 BMUF 和 Adam 的回顾,可以发现,如果不作任何处理直接将 Adam 嵌入 BMUF 框架,会面临 Adam 的一阶矩和二阶矩信息与模型参数不匹配的问题。假如我们设置很明显由于 ηΔ_n 的存在,一阶矩和二阶矩的平均对于下一 IBPO 的初始参数值来说已经陈旧。由于 ηΔ_n 的等效 minibatch 数目为 ηρ_n,因此我们认为,与 θ_t^((init)) 兼容的 m_t^((init)),v_t^((init)) 可以通过以 m ?_t,v ?_t 起始,处理 ηρ_n 个 minibatch 得到。其中 E[g^((n))] 表示第 n 次 IBPO 的 minibatch 随机梯度期望,因此
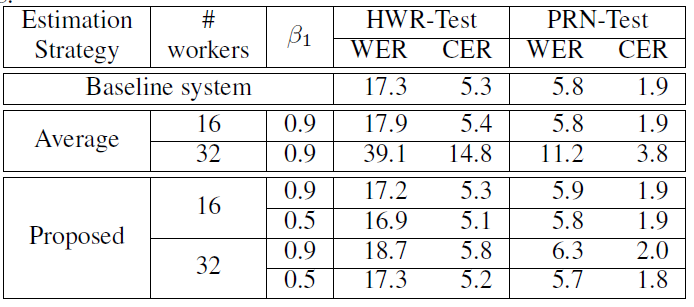
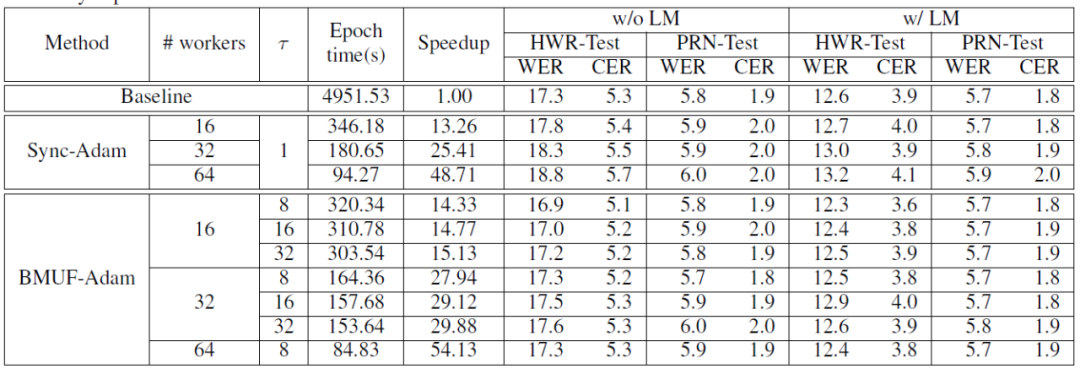
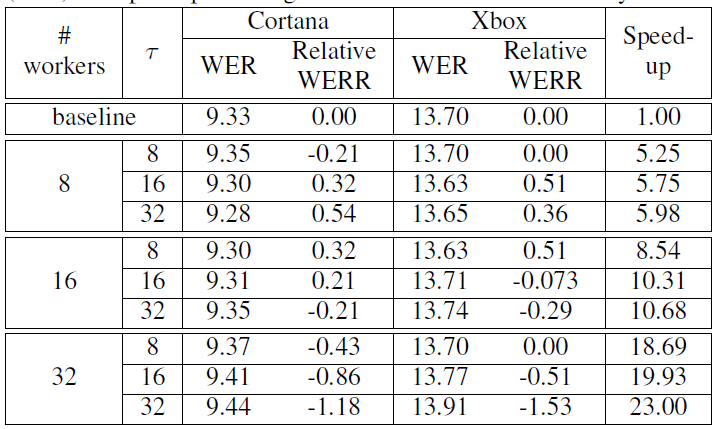
分析 m ?_t 和 m_t^((init)) 的计算公式,不难发现,当 τ 比较小而 N 比较大时,m_(t-τ)^((init)) 对 m ?_t 的过大贡献导致其与 θ_t^((init)) 的不一致现象更为严重,这一情况在我们的实验结果中得到了验证,而等效 minibatch 的引入,大大降低了 m_(t-τ)^((init)) 这一历史陈旧值对 m_t^((init)) 的贡献,可以起到改善模型性能的效果。同时,采用较小的 β_1 也能起到降低 m_(t-τ)^((init)) 贡献的作用。上述分析同样适用于二阶矩。最终我们得到 BMUF-Adam 算法如下:我们首先在微软大规模英文 OCR 任务上,对该方法进行了验证。首先比较将 Adam 嵌入 BMUF 框架时,采用不同矩估计策略的效果,结果如表1(该实验中模型同步周期?τ=8):我们发现,直接采用平均策略时,随着并行机器数目的增多,模型性能出现了明显下降,而我们提出的策略显著缓解了模型性能损失,而较小 β_1 的采用,显著提高了模型性能。接下来,在该任务上,我们对比了 Sync-Adam 和 BMUF-Adam,结果如表2:表2:Sync-Adam 和 BMUF-Adam 比较结果随着并行机器数目的增多,Sync-Adam 训练的模型出现了显著的性能下降,且训练数据处理的加速比明显变差。BMUF-Adam 在几乎线性加速模型训练的同时,基本不损失模型性能。同时我们还在微软基于6000小时语音训练数据集的语音识别任务上对 BMUF-Adam 算法进行了验证,结果如表3:BMUF-Adam 再次在基本不损失模型性能的前提下,实现了模型训练的几乎线性加速,展示出了优秀的可扩展性。?
我们在本文中采用 BMUF 框架对广泛使用的 Adam 算法进行了并行化,实验结果显示该算法相比传统的基于 SSG 的算法具有更快的训练速度,更好的模型性能,更优秀的可扩展性。该算法已应用于微软 OneOCR 和语音产品等多个产品中。https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9052983
关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/



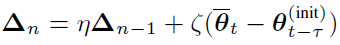
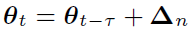
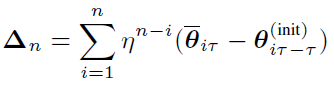
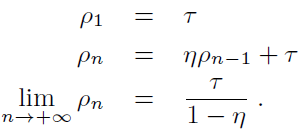
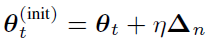
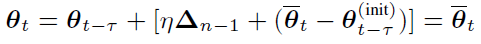
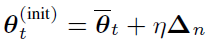

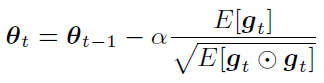
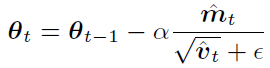
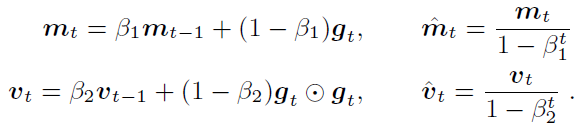

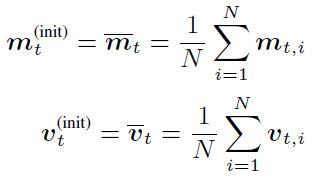
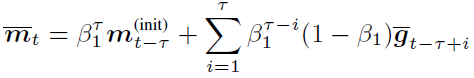
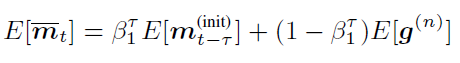

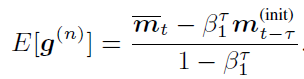
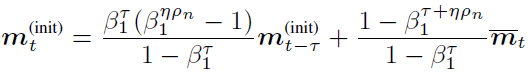







 关注网络尖刀微信公众号
关注网络尖刀微信公众号






 AI100
AI100







