选自arXiv
作者:Lisa Lee等
机器之心编译
机器之心编辑部
巨大的探索空间阻碍了强化学习(RL)的发挥,这篇论文通过弱监督学习从广泛的目标空间中分离出有语义意义的表征空间,从而增强 RL 的学习速度与泛化性能。
通用型智能体必须通过与真实环境交互来高效学习各种任务。典型的方法是人为地定义一组奖励函数,令智能体仅学习那些由奖励函数诱导出的任务。然而,定义与调整这些奖励函数需要耗费大量精力,并且使用者需要针对其关心的任务设置特定奖励函数,这为他们增添了额外的负担。而设计一个既能提供充足学习信号又能在算法收敛时诱导正确行为的奖励函数,是非常有挑战性的。最近,来自 CMU、谷歌大脑和斯坦福大学的研究者发布一项研究,展示了如何通过弱监督以最小负担为智能体提供有用信息,以及如何利用这些监督帮助智能体在环境中学习。研究者探索了一种在目标趋向强化学习(goal-conditioned RL)设置中使用弱监督的方法。研究者提出的弱监督智能体不需要通过探索和学习来达到每个目标状态,而是只需学习沿着有意义的变化轴达到相应状态,无需关注与解决人类指定任务无关的状态维度。重点是,研究者提出通过弱监督来执行此类约束,而不是列举目标或任务及其对应奖励。这项工作的主要贡献是弱监督控制(weakly-supervised control,WSC),这是一个将弱监督引入 RL 的简单框架。该方法学习一个有语义意义的表征空间,智能体可以使用该表征空间生成自己的目标,获取距离函数,并执行定向探索。WSC 包含两个阶段:首先基于弱标注离线数据学习状态的解纠缠表征,然后使用解纠缠表征约束 RL 智能体的探索空间。实验结果表明,学习解纠缠表征能够加快强化学习在多种操作任务上的学习速度,并提高其泛化能力。此外,研究者还发现 WSC 能够产生可解释的潜在策略(latent policy),其潜在目标直接与环境的可控特征保持一致。
论文链接:https://arxiv.org/abs/2004.02860研究者团队通过元组 (S, A, P, H, G) 定义有限时域下目标趋向的马尔可夫决策过程,其中 S 是观测空间,A 是动作空间,P (s′ | s, a) 表示一个未知动态函数,H 表示最大时间长度,G ? S 表示目标空间。在目标趋向 RL 中,研究者通过优化预期累积奖励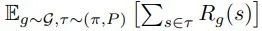 来训练策略 π_θ (a_t | s_t, g),从而在目标空间中达到目标 g?G,其中 R_g(s) 是由目标 g ∈ G 和观测值 s ∈ S 之间的距离度量定义的奖励函数。
来训练策略 π_θ (a_t | s_t, g),从而在目标空间中达到目标 g?G,其中 R_g(s) 是由目标 g ∈ G 和观测值 s ∈ S 之间的距离度量定义的奖励函数。
在低维度任务中,我们可以简单地将奖励视为状态空间中的负 ?_2 距离。然而,在高维度空间(如图像)中定义距离度量更具挑战性。先前关于视觉目标趋向(visual goal-conditioned)的 RL 工作训练了一个额外的状态表征模型,例如变分自编码器(VAE encoder)e^{VAE}:S→Z^{VAE}。这些方法基于编码状态和目标训练一个策略,并使用潜在空间中的 ?_2 距离来定义奖励函数: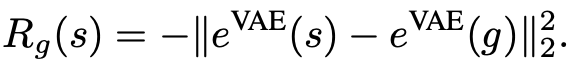
该研究提出的方法在 RL 环境中使用弱监督解纠缠表征学习。解纠缠表征学习旨在学习数据的可解释表征,表征的每一个维度度量一个独特的变化因子(factor of variation),这些因子是数据生成的基础(示例参见图 2)。
该研究使用一种叫作 rank pairing 的弱监督形式,其中数据集 D := {(s_1, s_2, y)} 由观测值 {s_1 , s_2 } 与弱二值化标签 y ∈ {0, 1}^K 组成,y_k = 1(f_k(s_1) < f_k(s_2)) 表示观测值 s_1 的第 k 个因子的值是否小于 s_2 的相应因子值。使用这些数据,Shu et al. (2019) 提出的弱监督方法通过优化以下损失函数训练出编码器 e : S → Z、生成器 G : Z → S 和判别器 D: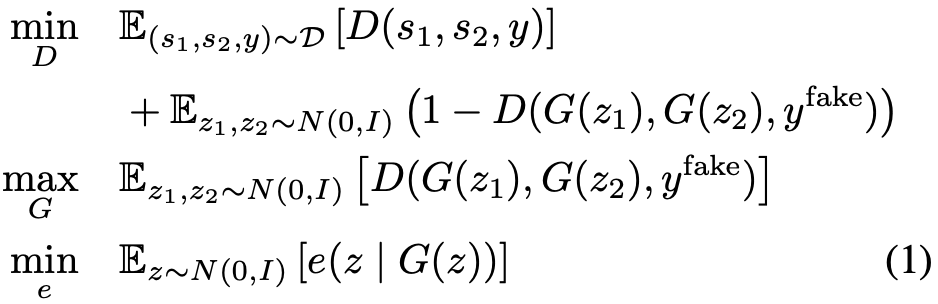
给定弱标注数据集 D: = {((s_1, s_2, y)},它由观测值 {s_1, s_2} 和弱二值化标签 y∈{0,1}^K 组成,其中 y_k = 1(f_k(s_1)<f_k(s2)) 表示观察值 s_1 的第 k 个因子值是否小于 s_2 的相应因子值。?除了这些标签外,使用者还可以指定索引子集 I ? [K],用来表示哪些因子(f_1,...,f_K)∈ F 与解决某一类任务有关。在训练期间,智能体可以与环境交互,但除了 D 中的弱标签外不接受任何监督(即没有奖励)。在测试阶段,采样未知的目标因子 f_I^? ∈ F_I,则智能体接收到目标观测(如目标图像),其因子等于 f_I^*。智能体的目标是学习 latent-conditioned RL 策略,以最小化目标距离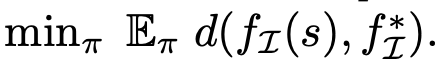 该研究提出的弱监督 RL 训练框架 WSC 包含两个阶段:首先基于弱标注离线数据学习状态的解纠缠表征,然后使用解纠缠表征来约束 RL 智能体的探索空间。
该研究提出的弱监督 RL 训练框架 WSC 包含两个阶段:首先基于弱标注离线数据学习状态的解纠缠表征,然后使用解纠缠表征来约束 RL 智能体的探索空间。
研究者提出的解纠缠表征学习基于上文介绍的 Shu et al. (2019) 方法构建。当然,理论上也可以使用其他类似的方法。该方法通过优化公式 1 中的损失函数来训练编码器、生成器和判别器。在训练完解纠缠模型后,研究者丢弃了生成器与判别器,仅用编码器来定义目标空间,并计算状态之间的距离。该研究提出的新方法将目标空间定义为学得的解纠缠潜在空间 Z_I,限制在索引 I 下。其目标采样分布的定义如下: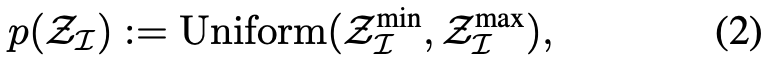
其中,Z^{min}_I 与 Z^{max}_I 分别表示对潜在值在元素层面上逐个取最小或最大。
在每一次迭代中,该方法从 p(Z_I) 中直接采样潜在目标 z_g,或从 replay buffer 中采样图像观测,并将其编码为解纠缠模型 z_g = e_I (s_g )。然后,执行该策略得到轨迹 (s_1, a_1, ..., s_T),从而尝试该目标。在基于 replay buffer 采样 transition (s_t, a_t, s_t+1, z_g) 时,研究者使用 hindsight re-labeling 和修改后的目标来提供额外的训练信号。也就是说,研究者有时会使用修改后的目标 z′_g 重新标注 transition (s_t, a_t, s_t+1, z′_g)。该方法将奖励函数定义为解纠缠潜在空间中的负 ?_2 距离: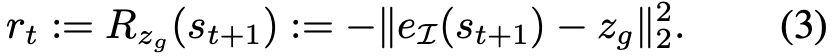

在图 4 中,研究者团队在 Sawyer 环境中的视觉目标趋向任务(参见图 2)上,对比了其提出的新方法和先前的 SOTA 目标趋向 RL 方法。
图 4:不同方法在视觉目标趋向任务上的性能随训练步的变化情况。弱监督控制(WSC)的学习速度超过之前的 SOTA 目标趋向 RL 方法(HER、RIG、SkewFit),尤其是在环境复杂性提高的情况下。因此,我们可以看到,在(学得的)语义解纠缠潜在空间中进行定向探索和目标采样比在 VAE 潜在空间中进行纯粹无监督的探索更加有效。在图 5 中,研究者评估了针对视觉目标趋向任务的训练策略,并比较了每个时间步上的潜在目标距离与真实目标距离。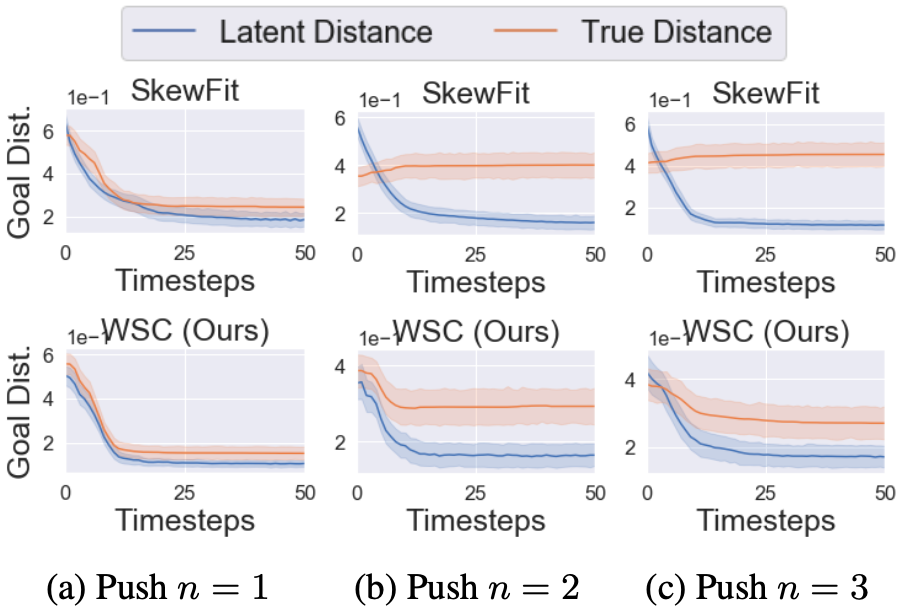
图 5:研究者针对视觉目标趋向的任务推出策略,并比较潜在目标距离与对象和目标位置之间的真实距离。随着环境变得越来越复杂(对象数量 n ∈ {1,2,3}),由 SkewFit 优化的潜在距离奖励越来越无法显示真实目标距离,而由 WSC 优化的解纠缠距离则更加准确。接下来,该研究测试了仅在解纠缠空间中的距离度量能否快速学习目标趋向任务。在图 6 中,我们看到解纠缠距离度量对较复杂的环境稍有帮助,但是与解纠缠潜在空间中具备目标生成机制的 WSC 完整方法相比性能不佳。
图 6:SkewFit + DR 是一种变体,它在 VAE 潜在空间中对目标进行采样,但使用的是解纠缠潜在空间中的奖励距离。我们从图中可以观察到, 解纠缠距离度量在较复杂的环境中(例如 Push n = 3)可能会有所帮助。但是相比之下,WSC 的目标生成机制对于实现有效的探索至关重要。机器之心 CVPR 2020 线上分享的第三期,我们邀请到腾讯优图实验室高级研究员 Louis 为我们做主题为《带噪学习和协作学习:不完美场景下的神经网络优化策略》的线上分享,欢迎读者报名学习。
关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/

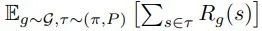 来训练策略 π_θ (a_t | s_t, g),从而在目标空间中达到目标 g?G,其中 R_g(s) 是由目标 g ∈ G 和观测值 s ∈ S 之间的距离度量定义的奖励函数。
来训练策略 π_θ (a_t | s_t, g),从而在目标空间中达到目标 g?G,其中 R_g(s) 是由目标 g ∈ G 和观测值 s ∈ S 之间的距离度量定义的奖励函数。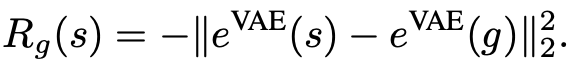

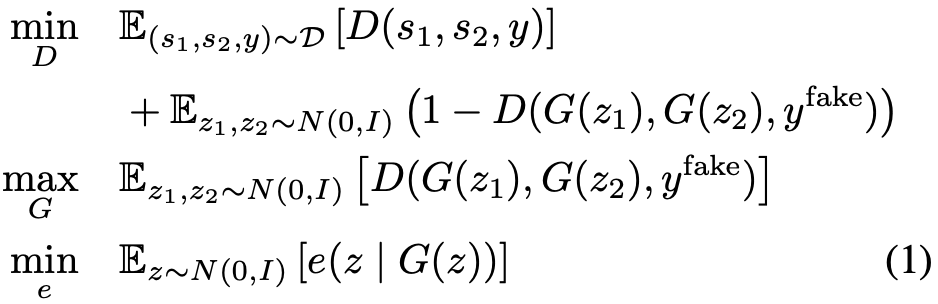
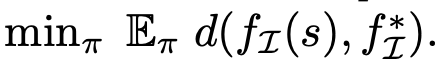

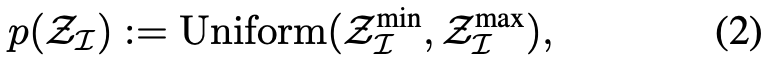
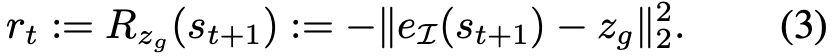





 关注网络尖刀微信公众号
关注网络尖刀微信公众号






 机器之心
机器之心







