吊打面试官系列:你会「递归」么?


递归,是一个非常重要的概念,也是面试中非常喜欢考的。因为它不但能考察一个程序员的算法功底,还能很好的考察对时间空间复杂度的理解和分析。
本文只讲一题,也是几乎所有算法书讲递归的第一题,但力争讲出花来,在这里分享四点不一样的角度,让你有不同的收获。
时空复杂度的详细分析
识别并简化递归过程中的重复运算
披上羊皮的狼

算法思路
大家都知道,一个方法自己调用自己就是递归,没错,但这只是对递归最表层的理解。
那么递归的实质是什么?
答:递归的实质是能够把一个大问题分解成比它小点的问题,然后我们拿到了小问题的解,就可以用小问题的解去构造大问题的解。
那小问题的解是如何得到的?
答:用再小一号的问题的解构造出来的,小到不能再小的时候就是到了零号问题的时候,也就是 base case 了。

那么总结一下递归的三个步骤:
Base case:就是递归的零号问题,也是递归的终点,走到最小的那个问题,能够直接给出结果,不必再往下走了,否则,就会成死循环;
拆解:每一层的问题都要比上一层的小,不断缩小问题的 size,才能从大到小到 base case;
组合:得到了小问题的解,还要知道如何才能构造出大问题的解。
所以每道递归题,我们按照这三个步骤来分析,把这三个问题搞清楚,代码就很容易写了。

斐波那契数列
这题虽是老生常谈了,但相信我这里分享的一定会让你有其他收获。
题目描述
斐波那契数列是一位意大利的数学家,他闲着没事去研究兔子繁殖的过程,研究着就发现,可以写成这么一个序列:1,1,2,3,5,8,13,21… 也就是每个数等于它前两个数之和。那么给你第 n 个数,问 F(n) 是多少。
解析
用数学公式表示很简单:
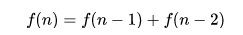
代码也很简单,用我们刚总结的三步:
base case: f(0) = 0, f(1) = 1. 分解:f(n-1), f(n-2) 组合:f(n) = f(n-1) + f(n-2)
class?Solution?{
????public?int?fib(int?N)?{
????????if?(N?==?0)?{
????????????return?0;
????????}?else?if?(N?==?1)?{
????????????return?1;
????????}
????????return?fib(N-1)?+?fib(N-2);
????}
}

过程分析
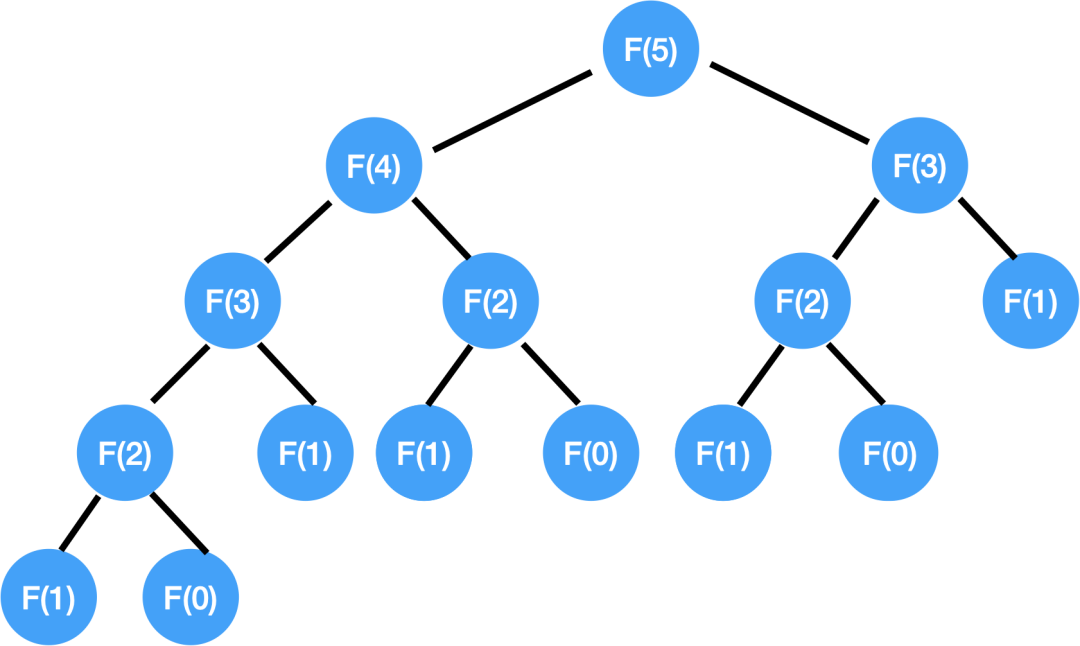

时间复杂度分析
如何评价一个算法的好坏?
时间复杂度:随着自变量的增长,算法所需时间的增长情况。
Theta: 描述的是 tight bound
Omega(n): 这个描述的是 best case,最好的情况,没啥意义
那对于这个题来说,时间复杂度是多少呢?
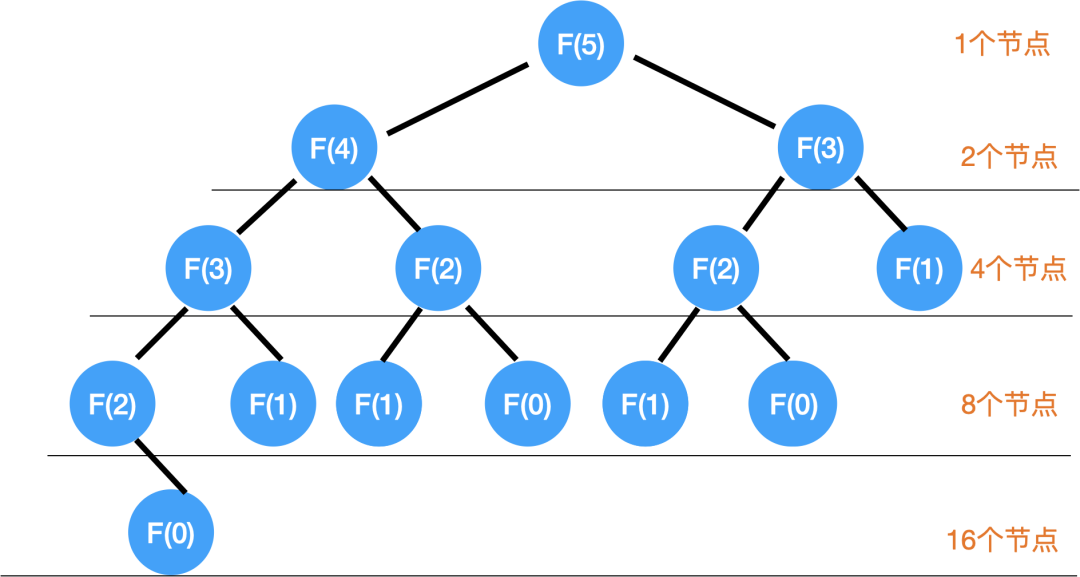
第二层 2 个,
第三层 4 个,
第四层 8 个,
第五层 16 个,如果填满的话,想象成一颗很大的树:)
1 + 2 + 4 + 8 + 16
空间复杂度分析
算法运行期间所需占用的所有内存空间
Auxiliary space complexity:
运行算法时所需占用的额外空间。
关注公众号:拾黑(shiheibook)了解更多
[广告]赞助链接:
四季很好,只要有你,文娱排行榜:https://www.yaopaiming.com/
让资讯触达的更精准有趣:https://www.0xu.cn/
 关注网络尖刀微信公众号
关注网络尖刀微信公众号随时掌握互联网精彩
- 1 确保“十五五”开好局起好步 7904829
- 2 员工“踢了一脚” 救了老板一命 7809229
- 3 故宫下雪了 7713121
- 4 2026年经济工作要这么干 7615817
- 5 村支书卖小米被小米法务投诉下架 7521444
- 6 女子买千元羽绒服穿1天变吸油服 7428950
- 7 直击北京初雪 7331024
- 8 凭煮蛋涨粉350万 “蛋神”回应爆红 7238101
- 9 茅台价格跌破1499元 7137353
- 10 中央经济工作会议释放哪些重要信号 7039913

![亦南南南 去年在厦门旅游时候拍的[赢牛奶] ](https://imgs.knowsafe.com:8087/img/aideep/2022/4/4/a89a8d23d94b622bf37f45a412fa12ca.jpg?w=250)





 程序人生
程序人生







