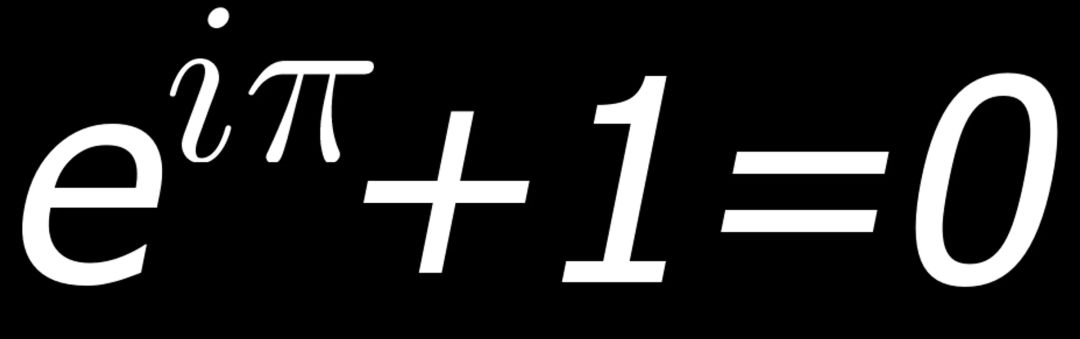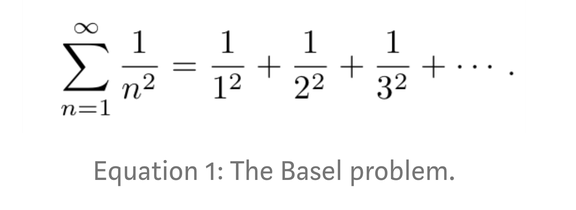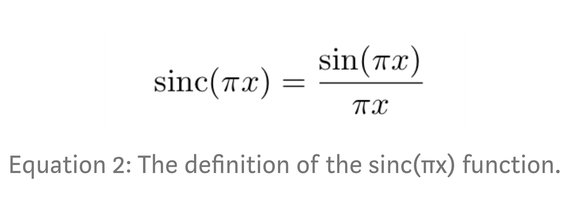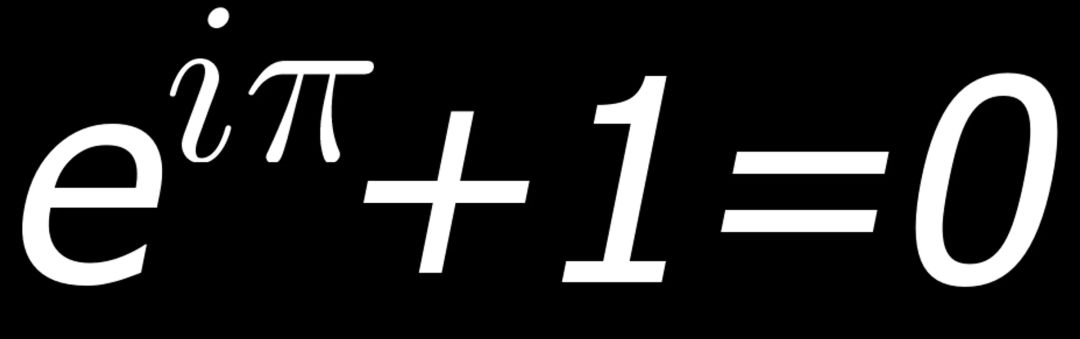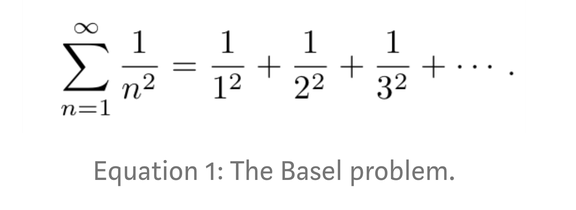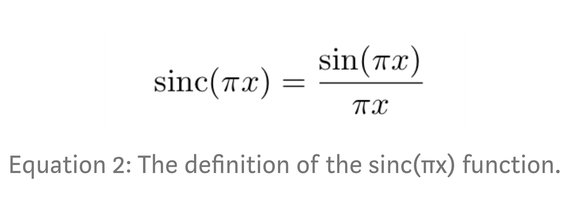什么是数学之美?就是思考的时候忘记时间的流逝,解答或证明后无与伦比的快乐。
欧拉,历史上最重要的数学家之一,也是最高产的数学家,平均每年能写八百多页论文。我们经常能见到以他名字命名的公式与定理,可能最广为人知的便是「世界上最美的公式」欧拉公式。先不说它的具体意义,能将自然数、虚数、π、0 和 1 这几个最基本的元素组合在一起,就是令人惊叹的美。欧拉公式将指数函数的定义域扩大到了复数域,同时建立三角函数和指数函数的关系,被誉为「数学中的天桥」。
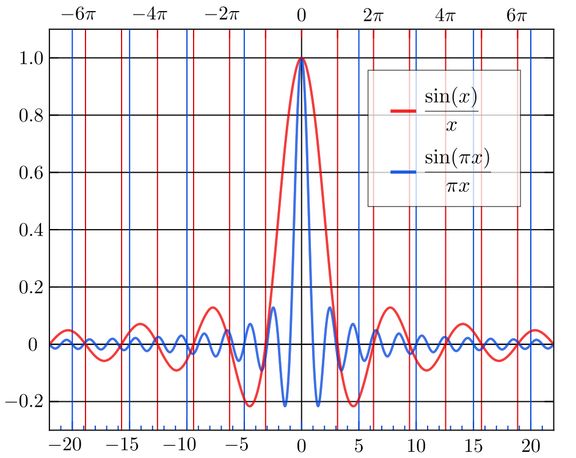
这样的数学方程是极具美感的,而要构建这样的方程,整个思考与推导过程同样是非常优美的。数学最吸引人的地方,就在于这一步步推导的过程,一种拨开云雾见月明的感觉。在本文中,我们希望通过一步步重现欧拉解巴塞尔问题的过程,体会到这种数学之美。巴塞尔问题是一个著名的数论问题,这个问题首先由皮耶特罗·门戈利在 1644 年提出,由欧拉在 1735 年解决。由于这个问题难倒了以前许多数学家,欧拉一解出这个问题马上就出名了,当时他二十八岁。这个问题是以瑞士的第三大城市巴塞尔命名的,为了纪念它是欧拉和伯努利家族的家乡。文章将解释欧拉是如何解决著名的巴塞尔问题的,看看如何用简单的 sin(x) 函数和多项式,再借助泰勒级数的强大能力,解决这个问题。巴塞尔问题起先在 1650 年就提出来了,它的目标在于求解某一离散无穷数列的和,具体来说,巴塞尔问题可以描述为如下:如果读者们还记得高数,记得无穷级数,你就会发现巴塞尔问题其实就是一个幂级数求和问题。当时很多学者都在想方法去计算这个问题,但欧拉在 28 岁时就证明了它,使得数学界非常惊叹。欧拉最初的证明方法并不一定是非常严格的,但它是非常优美的,简洁的过程与新奇的想法,使得我们能体会到「数学之美」。欧拉最初的想法来自 sinc(πx) 函数,他将该函数定义为如下:函数的图像如下所示,当 x 趋向于 0 时,因为 sin(x) 与 x 的速度等同,它们相除最终会收敛到 1。之所以要构造这个函数,答案就藏在它的零点,即当 sinc(πx) = 0 时 x 的所有取值。
*文章为作者独立观点,不代表 爱尖刀 立场
本文由
机器之心发表,转载此文章须经作者同意,并请附上出处(
爱尖刀 )及本页链接。
原文链接 https://www.ijiandao.com/2b/baijia/357007.html